x
Diferenciální rovnice
Obecné řešení
Najděme obecné řešení diferenciální rovnice y ‘= x
Definujme funkci dvou proměnných f(x,y) = 
x
Nyní najdeme obecné řešení diferenciální rovnice.
Obecné řešení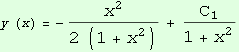 
, x ∈ R, 
∈ R
Partikulární řešení
Najděme partikukární řešení diferenciální rovnice y ‘= 
x
splňující počáteční podmínku y(1) = -
Partikulární řešení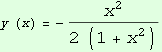 
, x ∈ R.
Integrální křivka
Nakresleme integrální křivku předchozího partikulárního řešení
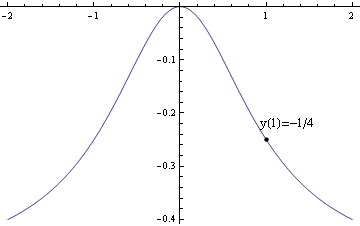
Aplikační příklad
Izotermní vnitřní difuze v porézním katalyzátoru je popsána diferenciální rovnicí 
= 
s okrajovými podmínkami y ’(0)=0 a y(1)=1, kde
y(x) je koncentrace,
a charakterizuje tvar částice katalizátoru (a=0,1,2 pro desku, váleček a kuličku)
n je řád reakce
φ Thieleho modul.
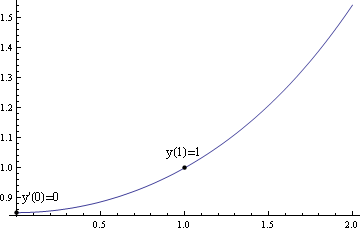
Nalezněme partikulární řešení pro parametry n=1, a=2, φ=1. Nakresleme integrální křivku partikulárního řešení
Nejdříve najdeme obecné řešení diferenciální rovnice.
Partikulární řešení diferenciální rovnice, splňující dané okrajové podmínky.
Definujeme partikulární řešení jako funkci
Partikulární řešení je 
, x ∈ R \ {0}.
Integrální křivka partikulárního řešení diferenciální rovnice. Podmínka y ’(0)=0 je splněna limitně, stejně tak hodnotu y(0) musíme vypočítat limitně.
Diferenciální rovnice - numerické (přibližné) řešení
Partikulární řešení
Najděme partikukární řešení diferenciální rovnice y ‘=
splňující počáteční podmínku y(0) = 1
Nejdříve zkusíme najít partikulární řešení diferenciální rovnice analyticky.
Protože jsme přesné řešení nenašly, najdeme numerické řešení diferenciální rovnice, protože víme, že řešení existuje.
Nedostaneme analytické řešení, ale můžeme si vypočítat přibližnou hodnotu v libovolném bodě z intervalu <0,1>.
Nebo si můžeme nakreslit přibližnou integrální křivku.
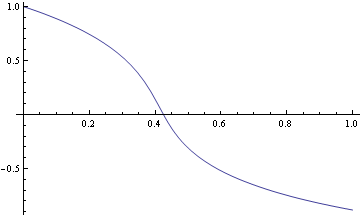
Aplikační příklad
Izotermní vnitřní difuze v porézním katalyzátoru je popsána diferenciální rovnicí 
= 
s okrajovými podmínkami y ’(0)=0 a y(1)=1, kde
y(x) je koncentrace,
a charakterizuje tvar částice katalizátoru (a=0,1,2 pro desku, váleček a kuličku)
n je řád reakce
φ Thieleho modul.
Nalezněme partikulární řešení pro parametry n=2, a=2, φ=1. Nakresleme integrální křivku partikulárního řešení
Numerické partikulární řešení diferenciální rovnice. Úloha je okrajová a nelze jednoduše numericky řešit. Musíme použít metodu střelby. Stačí nám výsledek s přesností na 5 desetinných míst.
Můžeme si vypočítat přibližnou hodnotu v libovolném bodě z intervalu <0,1>.
Můžeme si nakreslit přibližnou integrální křivku.
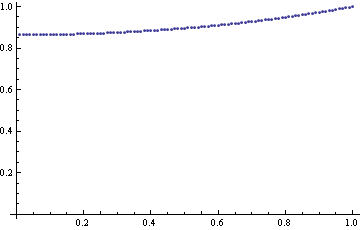
Přesvědčíme se, že jsme dostali “korektní řešení”. Malinko změníme okrajovou podmínku.
Můžeme si nakreslit přibližnou integrální křivku.
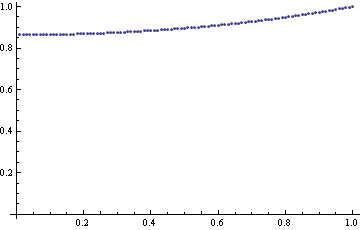
Zobrazíme si rozdíl obou řešení.
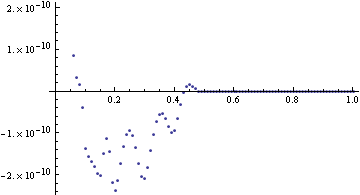
Vzhledem k tomu, že jsme požadovali řešení s přesností 
dá se předpokládat, že řeření je “korektní”. Při malé změně počáteční podmínky se řešení moc nezměnilo.
