Integrály
Vypočítejme některé složitější neurčité integraly
![]() , nakresleme graf fce f(x) a primitivní funkce F(x) na intervalu (-2,1)
, nakresleme graf fce f(x) a primitivní funkce F(x) na intervalu (-2,1)
In[1]:=
![]()
Out[1]=
![]()
In[2]:=
![]()
Out[2]=
![]()
Funkce není definovaná pro x=-2,1,2
In[3]:=
![]()
Out[3]=
![]()
In[4]:=
![]()
Out[4]=
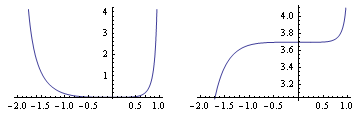
![]() , nakresleme graf fce f(x) a primitivní funkce F(x) na intervalu (-6,6)
, nakresleme graf fce f(x) a primitivní funkce F(x) na intervalu (-6,6)
In[5]:=
![]()
Out[5]=
![]()
In[6]:=
![]()
Out[6]=
![]()
Funkce je definovaná na celém R
In[7]:=
![]()
Out[7]=
![]()
In[8]:=
![]()
Out[8]=
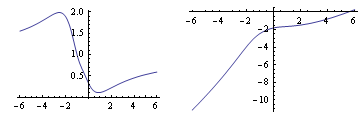
![]() , nakresleme graf fce f(x) a primitivní funkce F(x) na intervalu (-6,6)
, nakresleme graf fce f(x) a primitivní funkce F(x) na intervalu (-6,6)
In[9]:=
![]()
Out[9]=
![]()
Funkce je definovaná na celém R
In[10]:=
![]()
Out[10]=
![]()
In[11]:=
![]()
Out[11]=
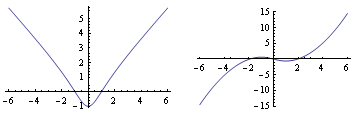
Vypočítejme plochu obrazce
Vypočtěme plochu obrazce ohraničeného grafem funkce y=x+sin(x), přímkou x=3π a osou x.
In[12]:=
![]()
Out[12]=
![]()
Nakreslíme si obrazec.
In[13]:=
![]()
Out[13]=
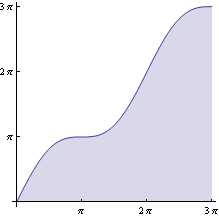
Vypočteme obsah pomocí integrálu ![]()
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
Out[15]=
![]()
Plocha obrazce je P =![]() = 46,4132
= 46,4132
Vypočtěme plochu obrazce ohraničeného grafem funkce ![]() a osou x.
a osou x.
In[16]:=
![]()
Out[16]=
![]()
Nejdříve najdeme průsečíky grafu s osou x.
In[17]:=
![]()
Out[17]=
![]()
Nakreslíme si obrazec.
In[18]:=
![]()
Out[18]=
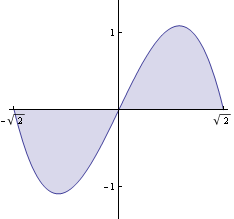
Vypočteme obsah pomocí integrálu (využijeme symetrie) P =2 ![]()
In[19]:=
![]()
Out[19]=
![]()
Plocha obrazce je P = 2.
Vypočtěme plochu obrazce ohraničeného grafem funkce y=x-x ln(1+x) , přímkou x=- ![]() a osou x.
a osou x.
In[20]:=
![]()
Out[20]=
![]()
Nejdříve najdeme průsečíky grafu s osou x.
In[21]:=
![]()
Out[21]=
![]()
Nakreslíme si obrazec.
In[22]:=
![]()
Out[22]=
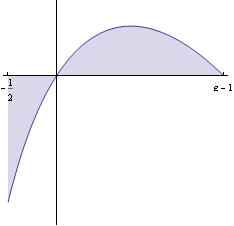
Vypočteme obsah pomocí integrálu P =- ![]() +
+ ![]()
In[23]:=
![]()
Out[23]=
![]()
In[24]:=
![]()
Out[24]=
![]()
In[25]:=
![]()
Out[25]=
![]()
Plocha obrazce je P = ![]() .
.
Vypočtěme plochu obrazce ohraničeného grafy funkcí ![]() , y =
, y = ![]() .
.
In[26]:=
![]()
Out[26]=
![]()
Out[27]=
![]()
Nejdříve najdeme průsečíky grafů.
In[28]:=
![]()
Out[28]=
![]()
Nakreslíme si obrazec.
In[29]:=
![]()
Out[29]=
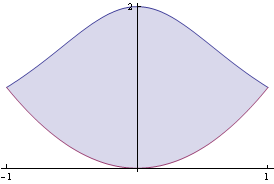
Vypočteme obsah pomocí integrálu (využijeme symetrie) P =2 ![]()
In[30]:=
![]()
Out[30]=
![]()
In[31]:=
![]()
Out[31]=
![]()
In[32]:=
![]()
Out[32]=
![]()
Plocha obrazce je P = ![]() .
.
Vypočítejme délku křivky (parametricky zadaná křivka)
Vypočtěme délku křivky x=2( t - t sin t)
y=2(1 - cos t), t ∈ <0,2 π> ,
In[33]:=
![]()
Out[33]=
![]()
Out[34]=
![]()
Nakreslíme si křivku.
In[35]:=
![]()
Out[35]=
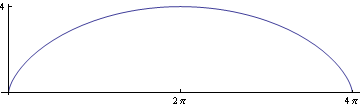
In[36]:=
![]()
Out[36]=
![]()
Out[37]=
![]()
Vypočteme délku pomocí integrálu ![]()
In[38]:=
![]()
Out[38]=
![]()
Out[108]=
![]()
Out[38]=
![]()
![]()
![]()
Výpočet neurčitého integrálu.
In[39]:=
![]()
Out[39]=
![]()
Výpočet délky křivk.
In[40]:=
![]()
Out[40]=
![]()
Délka křivky je l = 16.
Hmotný bod se pohybuje po dráze dané rovnicemi
x= 1 + sin 2 t
y=-1 + 3 sin t ,
Vypočítejte dráhu, kterou urazí hmotný bod od okamžiku ![]() =0 do okamžiku
=0 do okamžiku ![]() =π.
=π.
In[41]:=
![]()
Out[41]=
![]()
Out[42]=
![]()
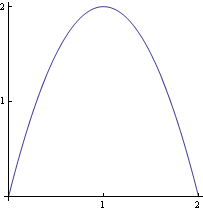
Nakreslíme si křivku.
In[43]:=
![]()
Out[43]=
In[44]:=
![]()
Out[44]=
![]()
Out[45]=
![]()
Vypočteme délku pomocí integrálu ![]()
In[46]:=
![]()
Out[46]=
![]()
Out[116]=
![]()
Out[46]=
![]()
![]()
Výpočet neurčitého integrálu.
In[47]:=
![]()
Out[117]=
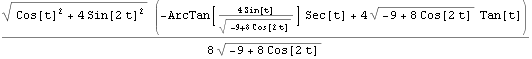
Výpočet délky křivk.
In[118]:=
![]()
Out[118]=
![]()
In[119]:=
![]()
Out[119]=
![]()
Délka křivky je l = ![]() .
.
Vypočítejme délku křivky, která je grafem funkce
Vypočtěme délku křivky, která je grafem funkce y=![]() , x ∈ <0, 1> ,
, x ∈ <0, 1> ,
In[120]:=
![]()
Out[120]=
![]()
Nakreslíme si graf.
In[121]:=
![]()
Out[121]=
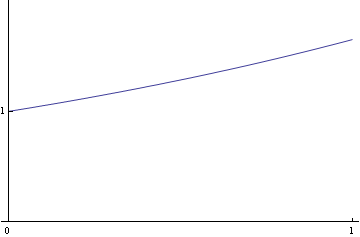
In[122]:=
![]()
Out[122]=
![]()
Vypočteme délku pomocí integrálu ![]()
In[123]:=
![]()
Out[123]=
![]()
Out[53]=
![]()
![]()
Výpočet neurčitého integrálu.
In[124]:=
![]()
Out[124]=
![]()
Výpočet délky křivky.
In[125]:=
![]()
Out[125]=
![]()
In[126]:=
![]()
Out[126]=
![]()
Délka křivky je l = ![]() .
.
Vypočítejme objem rotačního tělesa
Vypočtěme objem tělesa, které vznikne rotací plochy ohraničené grafem funkce y=sin x, x ∈ <0, π> a osy x kolem osy x.
In[127]:=
![]()
Out[127]=
![]()
Nakreslíme si plochu.
In[128]:=
![]()
Out[128]=
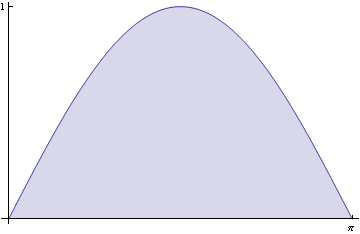
Vypočteme objem pomocí integrálu ![]()
Výpočet objemu.
In[129]:=
![]()
Out[129]=
![]()
Objem rotačního telesa je V = ![]() .
.
Vypočtěme objem tělesa, které vznikne rotací plochy ohraničené grafem funkce y=![]() , x ∈ <-1,1> a osy x kolem osy x.
, x ∈ <-1,1> a osy x kolem osy x.
In[130]:=
![]()
Out[130]=
![]()
Nakreslíme si plochu.
In[131]:=
![]()
Out[131]=
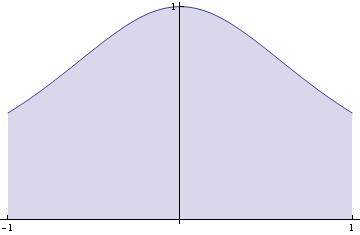
Vypočteme objem pomocí integrálu ![]()
Výpočet objemu.
In[132]:=
![]()
Out[132]=
![]()
In[133]:=
![]()
Out[133]=
![]()
Objem rotačního telesa je V = ![]() 2.43733.
2.43733.
Vypočtěme objem tělesa, které vznikne rotací plochy ohraničené grafem funkce y= tg x, x ∈ <0, ![]() > a osy x kolem osy x.
> a osy x kolem osy x.
In[134]:=
![]()
Out[134]=
![]()
Nakreslíme si plochu.
In[135]:=
![]()
Out[135]=
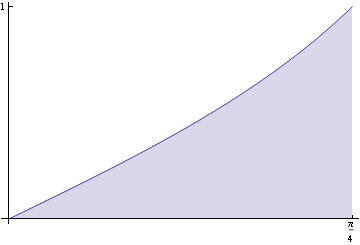
Vypočteme objem pomocí integrálu ![]()
Výpočet objemu.
In[136]:=
![]()
Out[136]=
![]()
In[137]:=
![]()
Out[137]=
![]()
Objem rotačního telesa je V = ![]() 0.674192.
0.674192.
Vypočtěme objem elipsoidu s osami a, b, a.
Jedná se o rotační těleso, kde rotuje plocha ohraničená půlelipsou a osou . Umístíme vhodně elipsu do souřadnicového systému.
Předpis pro funkci, jejíž grafem je půlelipsa je y = 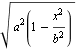 .
.
In[138]:=
![]()
Out[138]=
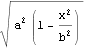
Nakreslíme si plochu pro a=1 a b=2.
In[139]:=
![]()
Out[139]=
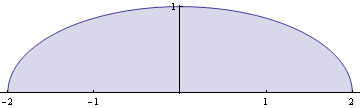
Vypočteme objem pomocí integrálu ![]()
Výpočet objemu.
In[140]:=
![]()
Out[140]=
![]()
Objem elipsoidu s osami a, b, a je V =![]() .
.