= x ‘= x+2y
= y ‘= -2 x+y
Soustavy diferenciálních rovnic
Autonomní soustavy lineárních rovnic
Obecné řešení
Najděme obecné řešení soustavy diferenciálních rovnic = x ‘= x+2y= y ‘= -2 x+y
Definujme soustavu funkcí dvou proměnných
f1(x,y) = x + 2 y
f2(x,y) = - 2 x + y
Nyní najdeme obecné řešení soustavy diferenciálních rovnic.
Obecné řešení
, t ∈ R, 
,
∈ R
Partikulární řešení autonomní soustavy lineárních rovnic
Najděme obecné řešení soustavy diferenciálních rovnic 
= x ‘= x+2y
= y ‘= -2 x+y
splňující počáteční podmínky x(0) =1, y(0) = 0
Partikulární řešení 
t ∈ R.
Integrální křivky
Nakresleme integrální křivky předchozího partikulárního řešení
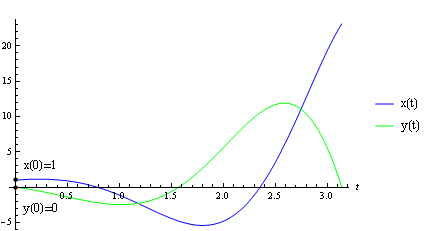
Trajektorie
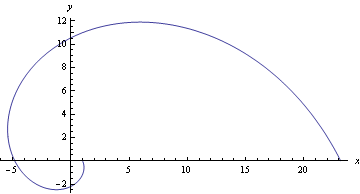
Nakresleme trajektorii předchozího partikulárního řešení
Neautonomní soustavy lineárních rovnic
Obecné řešení
Najděme obecné řešení soustavy diferenciálních rovnic 
= x ‘= x+ 2 y + 
= y ‘= -2 x+ y + 
Definujme soustavu funkcí dvou proměnných
f1(x,y) = x + 2 y + 
f2(x,y) = - 2 x + y + 
Nyní najdeme obecné řešení soustavy diferenciálních rovnic.
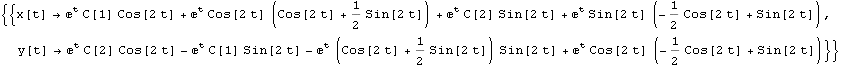
Obecné řešení
y(t)= 
t ∈ R, 
,
∈ R
Partikulární řešení autonomní soustavy lineárních rovnic
Najděme obecné řešení soustavy diferenciálních rovnic 
= x ‘= x + 2 y + 
= y ‘= -2 x + y + 2 
splňující počáteční podmínky x(0) =1, y(0) = 0
Partikulární řešení 
t ∈ R.
Integrální křivky
Nakresleme integrální křivku předchozího partikulárního řešení
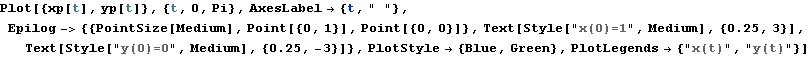
Trajektorie
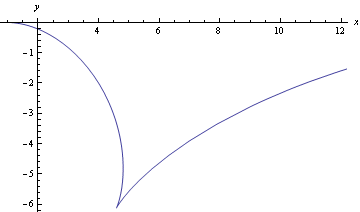
Nakresleme trajektorii předchozího partikulárního řešení
Soustavy diferenciálních rovnic - numerické (přibližné) řešení
Autonomní soustavy nelineárních rovnic
Partikulární řešení
Najděme partikukární řešení soustavy diferenciálních rovnic
x ‘=
y ’ = x y
splňující počáteční podmínku x(0) = 1, y(0)=1
Nejdříve zkusíme najít partikulární řešení diferenciální rovnice analyticky.
Protože jsme přesné řešení nenašly, najdeme numerické řešení soustavy diferenciálních rovnic, protože víme, že řešení existuje (z věty o jednoznačnosti a existenci).
Nedostaneme analytické řešení, ale můžeme si vypočítat přibližnou hodnotu v libovolném bodě z intervalu <0,1>.
Tabulka řešení
Můžeme vypsat tabulku hodnot řešení na intervalu <0,1>.
| t | x[t] | y[t] |
| 0. | 1. | 0. |
| 0.1 | 0.908749 | 0.10484 |
| 0.2 | 0.830513 | 0.218761 |
| 0.3 | 0.759415 | 0.340872 |
| 0.4 | 0.690289 | 0.470153 |
| 0.5 | 0.618357 | 0.605251 |
| 0.6 | 0.539062 | 0.744248 |
| 0.7 | 0.448035 | 0.88443 |
| 0.8 | 0.341149 | 1.02208 |
| 0.9 | 0.214663 | 1.15237 |
| 1. | 0.0653834 | 1.26945 |
Integrální křivky
Nebo si můžeme nakreslit přibližné integrální křivky.
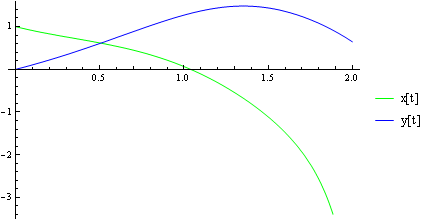
Trajektorie řešení
Můžeme si nakreslit také přibližnou trajektorii řešení.
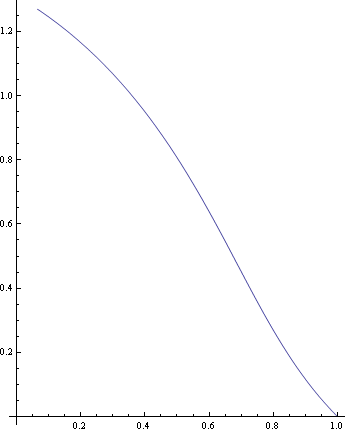
Aplikační příklad
Model dravec-kořist
Model dravec-kořist (viz Matematica II) lze popsat soustavou diferenciálních rovnic
= a x - α x y
= -b y+ β x y
s počátečními podmínkami x(0)=
a y(0)=
,
kde x(t) je množství kořisti a y(t) je množství dravců,
Koeficienty a, b, α, β viz Matematica II.
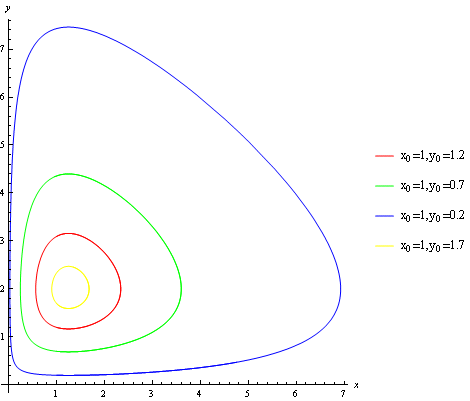
Nalezněme partikulární řešení pro parametry a=2, b=1, α=1, β=0.8. Nakresleme trajektorie partikulárního řešení pro různé hodnoty počátečních podminek.
Najdeme numericky partikulární řešení soustavy diferenciálních rovnic pro počáteční podmínky x(0)=1 a y(0)= 0.2.
Vykreslíme trajektorii řešení pro počáteční podmínky x(0)=1 a y(0)= 0.2.
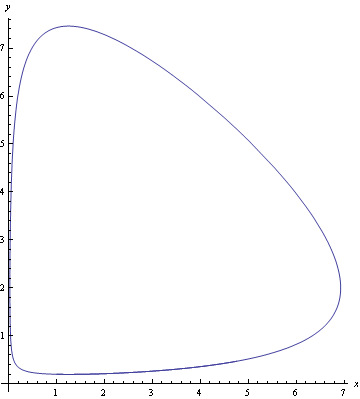
Najdeme numericky partikulární řešení soustavy diferenciálních rovnic pro počáteční podmínky
x(0)=1 a y(0)= 0.2
x(0)=1 a y(0)= 0.7
x(0)=1 a y(0)=1.2
x(0)=1 a y(0)= 1.7.
Vykreslíme všechny trajektorie.
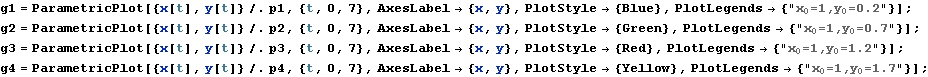
