Dvojné integrály
Vypočítejme některé dvojnásobné integrály
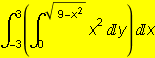
Vypočítejme dvojný integrál
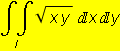, kde I = <0,1>×<0,3>
Podle Fubiniovy věty převedeme na dvojnásobný integrál.
Výsledek V =
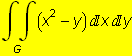, kde G ={{x,y}∈ 
, -1≤ y ≤ 1+
∧ -1 ≤ x ≤ 1}
Nakreslíme si množinu G
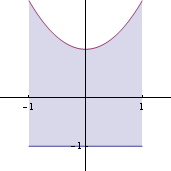
Napšeme si dvojný integrál jako dvojnásobný.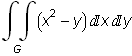 
= 
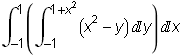
Dvojnásobný integrál nám už vypočte Mathematica
Výsledek V =
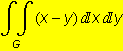, kde G je ohraničena přímkami x = -1, x = 1, y = x-1 a parabolou y = 
.
Nakreslíme si oblast G.
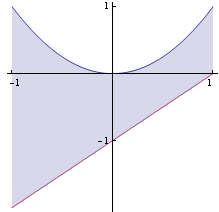
Převedení na dvojnásobný integrál podle Fubiniovy věty musíme udělat my.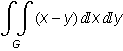 
= 
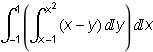. Dvojnásobný integrál nám už vypočte Mathematica
Výsledek V =
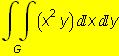, kde G je ohraničena přímkami y = x + 1, y = x, y = -2x + 1, y = -2x+5
Nakreslíme si množinu G
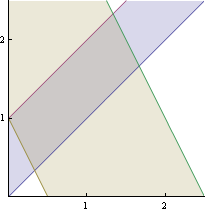
Hledáme průsečíky přímek:
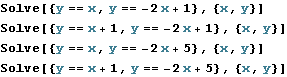
Napíšeme si dvojný integrál jako dvojnásobné integrály: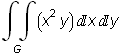 
= 
+ 
+ 
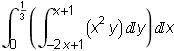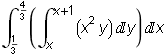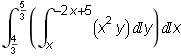
Vypočteme dvojnásobné integrály.
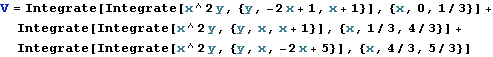
Výsledek V =
Substituce pro dvojný integrál
Vypočtěme dvojný integrál 
, kde D = {(x,y)∈
; 
≤ 1} .
Nakreslíme si množinu D.
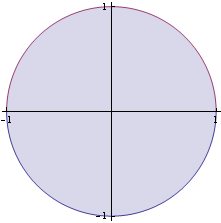
Můžeme použít Fubiniovu větu a převést dvojný integrál na dvojnásobný 
dy =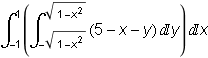 
Vypočteme dvojnásobný integrál:
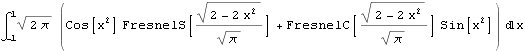
Tento příkaz je stejný, jako když vnější integrál vypočtete numericky:
Nedostali jsme uspokojivý výsledek (dostali jsme pouze přibližný výsledek).
Použijeme substituci do polárních souřadnic:
x = r cos t,
y = r sin t, r ∈<0,∞>, t ∈ <0, 2 π>.
Množina D přejde substitucí na množinu H = <0,1>×<0,2π>. Jakobián pro polární souřednice je r. Dostaneme tedy
dy = 
dt = 
Vypočteme nyní dvojnásobný integrál:
Výsledek V = 
= 1.44418.
Vypočítejme objem tělesa
Vypočtěme objem tělesa ohraničeného rovinami x = 0, y = 0, z = 0, x = 2, y = 3, x + y + z = 5.
Nakreslíme si těleso.
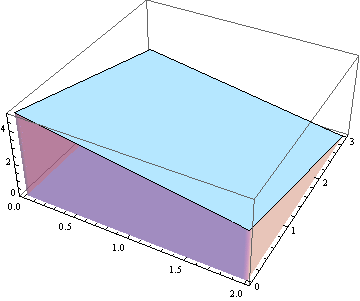
Vypočteme objem pomocí integrálu 
dy
Oblast G, přes kterou integrujeme je obdelník <0,2>×<0,3>. Můžeme hned použít Fubiniovu větu a převést dvojný integrál na dvojnásobný 
dy = 
Výpočteme objem.
Objem tělesa je V = 15.
Vypočtěme objem tělesa ohraničeného plochou y = 
a rovinami z = 0, y + z = 2.
Nakreslíme si těleso.
Plocha y = 
.
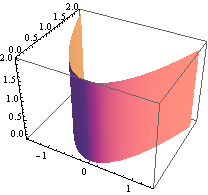
Roviny z = 0, y + z = 2 .
Průnik ploch.
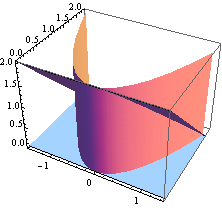
Teď se pokusíme nakreslit těleso:
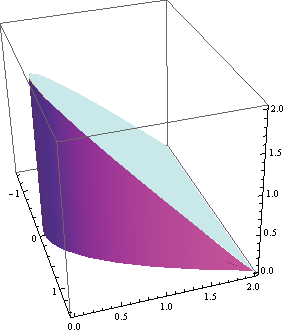
Vypočteme objem pomocí integrálu 
dy
Oblast G, přes kterou integrujeme je množina {(x,y)∈
; y ≥
∧y≤2 } . Oblast si nakreslíme.
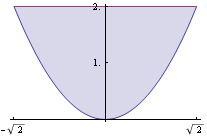
Můžeme hned použít Fubiniovu větu a převést dvojný integrál na dvojnásobný 
dy = 
Výpočteme objem.
Objem tělesa je V = 
.
Vypočtěme objem tělesa ohraničeného plochami z = 
+
, y = 
a rovinami y =1, z = 0.
Nakreslíme si těleso.
Plocha z = 
+
.
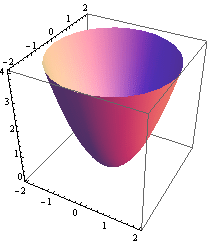
Plocha y = 
.
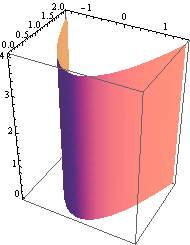
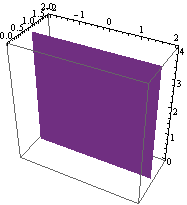
Rovina y =1.
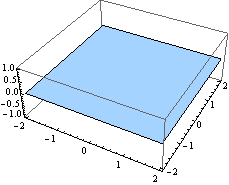
Rovina z =0.
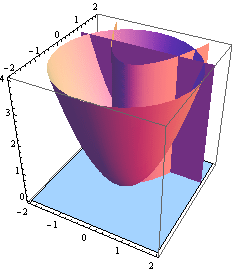
Průnik ploch:
Teď se pokusíme nakreslit těleso:
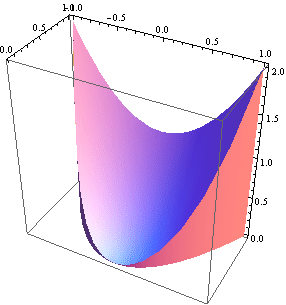
Vypočteme objem pomocí integrálu 
dy
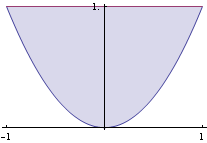
Oblast G, přes kterou integrujeme je množina {(x,y)∈
; y ≥
∧y≤1 } . Oblast si nakreslíme.
Můžeme hned použít Fubiniovu větu a převést dvojný integrál na dvojnásobný 
dy = 
Výpočteme objem.
Objem tělesa je V = 
.
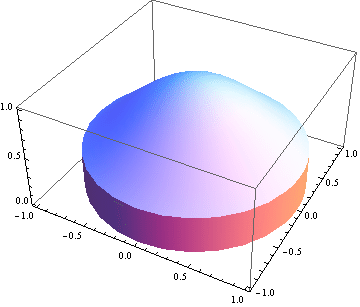
Vypočtěme objem tělesa ohraničeného plochami z = 
, 
+
= 1 a rovinou z = 0.
Nakreslíme si těleso. Nejdříve nakreslíme jednotlivé plochy.
Plocha 
+
= 1.
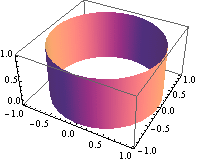
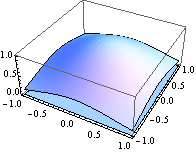
Graf funkce z = 
a rovina z = 0.
Průnik ploch.
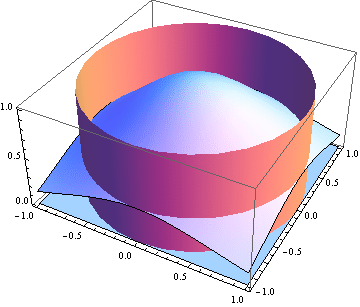
A teď celé těleso.
Vypočteme objem pomocí integrálu 
dy
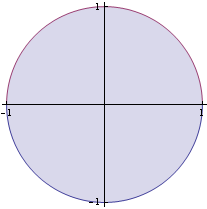
Uzavřená oblast G, přes kterou integrujeme je množina {(x,y)∈
; 
≤ 1} . Oblast si nakreslíme.
Můžeme hned použít Fubiniovu větu a převést dvojný integrál na dvojnásobný (využijeme symetrie) 
dy = 4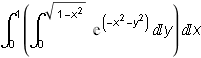
Výpočteme objem.
Mathematica nám integrál vypočte pouze přibližně, chceme-li dostat přesný výpočet, musíme použít substituci: x = r cos t, y = r sin t
Počítáme tedy integrál 
dt, kde M je množina (0,1> × <0,2 π)
Můžeme použít Fubiniovu větu a převést dvojný integrál na dvojnásobný 
dt = 
Objem tělesa je V = 
.
