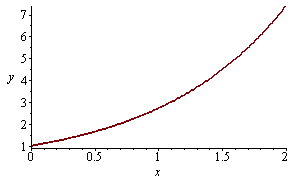Symbolicka matematika
Funkce
Tabulka elementárních finkcí:
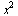
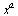
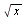
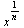
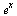 ln(x) log(x) log a (x)
ln(x) log(x) log a (x)
x^2 x^a sqrt(x) x^(1/n) exp(x) ln(x) log10 (x) log[a](x)
sin(x) cos(x) tg(x) cotg(x) arcsin(x) arccos(x) arctg(x) arccotg(x)
sin(x) cos(x) tan(x) cot(x) arcsin(x) arccos(x) arctan(x) arccot(x)
sinh(x) cos h(x) tgh(x) cotgh(x) |x| sgn(x) 1/x
sinh(x) cos h(x) tanh(x) coth(x) abs(x) sgn(x) 1/x
Vlastní definice funkce f(x)
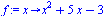 |
(2.1.1) |
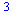 |
(2.1.2) |
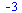 |
(2.1.3) |
Vlastní definice funkce f(x)=x^2 je-li x<0 a x je-li x>=0
| > |
v:=piecewise(x < 0,x^2,x>=0,x); |
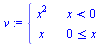 |
(2.1.4) |
| > |
f:=x->piecewise(x < 0,x^2,x>=0,x); |
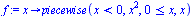 |
(2.1.5) |
 |
(2.1.6) |
 |
(2.1.7) |
 |
(2.1.8) |
Derivace
první derivace f '(x)
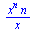 |
(2.2.1) |
třetí derivace f '''(x)
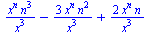 |
(2.2.2) |
Parciální derivace funkce f(x,y) podle x
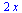 |
(2.2.3) |
Parciální derivace funkce f(x,y) podle y
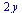 |
(2.2.4) |
Jiná možnost derivace (máme-li definovanou funkci)
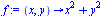 |
(2.2.5) |
Derivace podle první proměnné
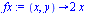 |
(2.2.6) |
Derivace podle druhé proměnné
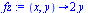 |
(2.2.7) |
Integrace
Primitivní funkce
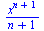 |
(2.3.1) |
Příkaz s velkým začátečním písmenem vypíše pouze symbol integrálu (můžeme ho používat pro přehlednější zápis)
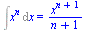 |
(2.3.2) |
 |
(2.3.3) |
| > |
Int(1/(x^4-a^4),x)=int(1ralu/(x^4-a^4),x); |
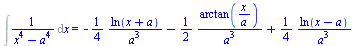 |
(2.3.4) |
F je primitivní funkce zapsaná v Maple jako funkce
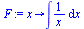 |
(2.3.5) |
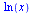 |
(2.3.6) |
Pozor !!! Maple obecně počítá v komplexním obor, kde je definovaný logaritmus ze záporného čísla. Proto také předchozí výsledek není ln(|x|)
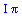 |
(2.3.7) |
Určitý integrál z funkce f(x) od a do b
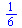 |
(2.3.8) |
| > |
Int(x^5,x=0..1)=int(x^5,x=0..1); |
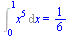 |
(2.3.9) |
Nevlastní integrály
1. integrál diverguje
| > |
Int(1/x,x=0..1)=int(1/x,x=0..1); |
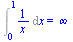 |
(2.3.10) |
| > |
Int(1/x,x=1..infinity)=int(1/x,x=1..infinity); |
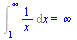 |
(2.3.11) |
2. integrál konverguje
| > |
Int(1/x^2,x=0..infinity)=int(1/x^2,x=1..infinity); |
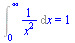 |
(2.3.12) |
| > |
Int(x^n,x=0..1)=int(x^n,x=0..1); |
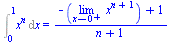 |
(2.3.13) |
| > |
Int(x^n,x=0..1)=int(x^n,x=0..1); |
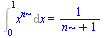 |
(2.3.14) |
| > |
Int(x^n,x=0..1)=int(x^n,x=0..1); |
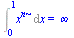 |
(2.3.15) |
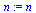 |
(2.3.16) |
Někdy promitivní funkci Maple nevypočte (neznamená to, že neexistuje):
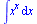 |
(2.3.17) |
Suma
Součet nekonečné řady:
| > |
sum(1/2^n,n=1..infinity); |
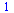 |
(2.4.1) |
| > |
Sum(1/2^n,n=1..infinity)=sum(1/2^n,n=1..infinity); |
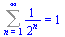 |
(2.4.2) |
| > |
Sum(1/n!,n=1..infinity)=sum(1/n!,n=1..infinity); |
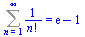 |
(2.4.3) |
| > |
Sum(1/x^n,n=1..infinity)=sum(1/x^n,n=1..infinity); |
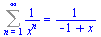 |
(2.4.4) |
Pozor !!!! Maple nám neřekne pro která x součet platí. V tomto případě to plati pro |x|>1. Například si můžeme ukázat, že pro x=1/2 nebo x = -1 řada diverguje.
| > |
Sum(1/(1/2)^n,n=1..infinity)=sum(1/(1/2)^n,n=1..infinity); |
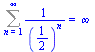 |
(2.4.5) |
| > |
Sum(1/(-1)^n,n=1..infinity)=sum(1/(-1)^n,n=1..infinity); |
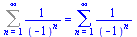 |
(2.4.6) |
Maple nám neřekne, že diverguje, ale jednoduchou úvahou (sudé a liché částečné součty) zjistíme, že součet řady neexistuje.
Limity
limita f(x) když x se blíží k a
 |
(2.5.1) |
| > |
Limit(sin(x),x=0)=limit(sin(x),x=0); |
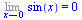 |
(2.5.2) |
| > |
Limit(1/x,x=0)=limit(1/x,x=0); |
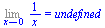 |
(2.5.3) |
limita f(x) když x se blíží k a zprava
| > |
Limit(1/x,x=0,right)=limit(1/x,x=0,right); |
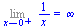 |
(2.5.4) |
limita f(x) když x se blíží k a zleva
| > |
Limit(1/x,x=0,left)=limit(1/x,x=0,left); |
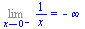 |
(2.5.5) |
Řešení rovnic
Řešení alg. rovnic
| > |
v:=solve(x^2+2*x-7=0,x); |
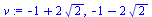 |
(3.1.1) |
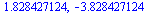 |
(3.1.2) |
| > |
v1:=solve(x^2+a*x+b=0,x); |
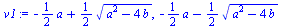 |
(3.1.3) |
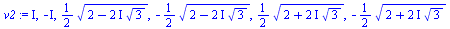 |
(3.1.4) |
| > |
v3:=solve(x^5-2*x^3+x^2+3*x-1=0,x); |
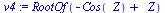 |
(3.1.6) |
V případě, že nelze najit řešení rovnice analiticky, je třeba použít numerické řešení (viz Numerická matematika)
Řešení diferenciálních rovnic
Obecné řešení
| > |
dsolve(diff(y(x),x)=1+y(x),y(x)); |
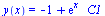 |
(3.2.1) |
Partikulární řešení splňující počáteční podmínku
| > |
dsolve({diff(y(x),x)=1+y(x),y(0)=1},y(x)); |
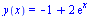 |
(3.2.2) |
Obecné řešení
| > |
dsolve(diff(y(x),x)=1/y(x),y(x)); |
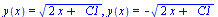 |
(3.2.3) |
Partikulární řešení splňující počáteční podmínku
| > |
res:=dsolve({diff(y(x),x)=1/y(x),y(0)=1},y(x)); |
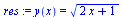 |
(3.2.4) |
| > |
plot(rhs(res),x=-0.5..1); |
Pozor Maple nás neupozorní, že řešení není definované v bodě x=0.5
Obecné řešení soustavy rovnic
| > |
dsolve({diff(x(t),t)=-y(t),diff(y(t),t)=x(t)},{x(t),y(t)}); |
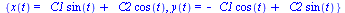 |
(3.2.5) |
Partikulární řešení splňující počáteční podmínku
| > |
res1:=dsolve({diff(x(t),t)=-y(t),diff(y(t),t)=x(t),x(0)=1,y(0)=0},{x(t),y(t)}); |
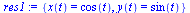 |
(3.2.6) |
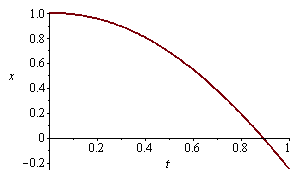
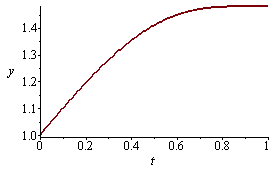
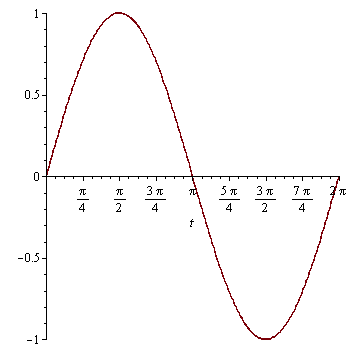
Nakreslení integrální křivky (graf partikulárního řešení x(t))
Nakreslení integrální křivky (graf partikulárního řešení y(t))
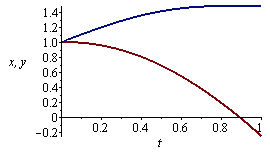
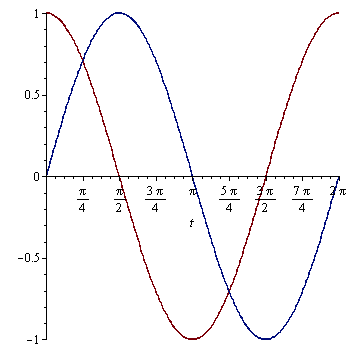
Nakreslení integrálních křivek do jednoho obrázku
| > |
plot([x(t),y(t)],t=0..2*Pi); |
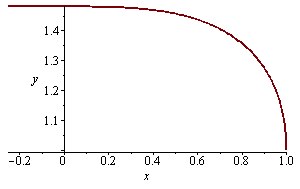
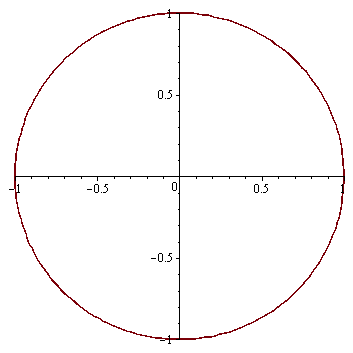
Nakreslení trajektorie řešení (graf parametricky zadané křivky)
| > |
plot([x(t),y(t),t=0..2*Pi]); |
Grafy
Grafy 2D
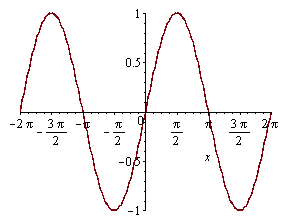
Nejjednodušší vykreslení grafu.
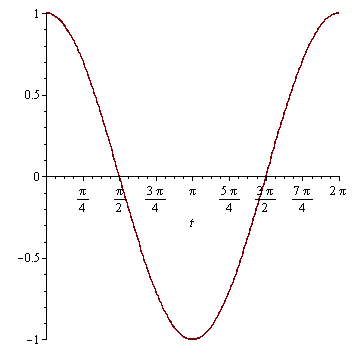
| > |
plot(sin(x),x=-2*Pi..2*Pi); |
Teď použijeme různé volby (options).
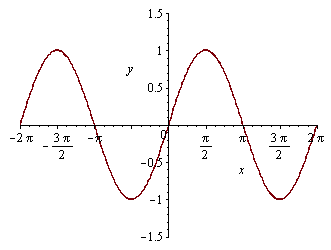
1. Rozsah osy y
| > |
plot(sin(x),x=-2*Pi..2*Pi,y=-1.5..1.5); |
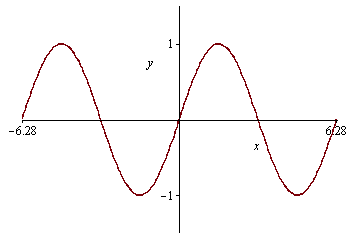
2. Číselný popis osy x a y
| > |
plot(sin(x),x=-2*Pi..2*Pi,y=-1.5..1.5,tickmarks=[[-6.28,0,6.28], [-1, 1]]); |
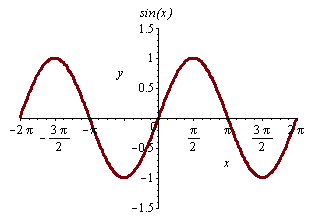
3. Tloušťka čáry a titulek.
| > |
plot(sin(x),x=-2*Pi..2*Pi,y=-1.5..1.5,thickness=3,title=`sin(x)`); |
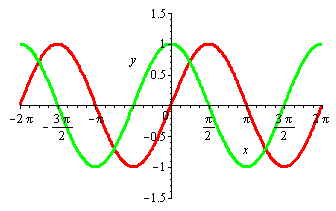
4. Grafy více funkcí do jednoho obrázku a barva grafu.
| > |
plot([sin(x),cos(x)],x=-2*Pi..2*Pi,y=-1.5..1.5,thickness=3,color=[red,green]); |
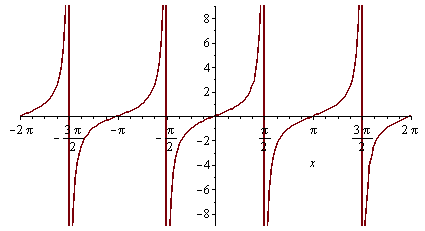
5. Pozor při kreslení grafu některých funkcí (nakreslí čáry navíc)
| > |
plot(tan(x),x=-2*Pi..2*Pi); |
| > |
plot(tan(x),x=-2*Pi..2*Pi,discont=true); |
Parametrické grafy 2D
| > |
plot([cos(x),sin(2*x),x=0..2*Pi]); |
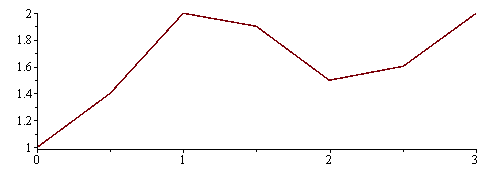
Zobrazení dat do grafu
| > |
data:=[[0,1],[0.5,1.4],[1.0,2.0],[1.5,1.9],[2.0,1.5],[2.5,1.6],[3.0,2.0]]; |
![[[0, 1], [.5, 1.4], [1.0, 2.0], [1.5, 1.9], [2.0, 1.5], [2.5, 1.6], [3.0, 2.0]]](images/ManualMaple_95.gif) |
(4.3.1) |
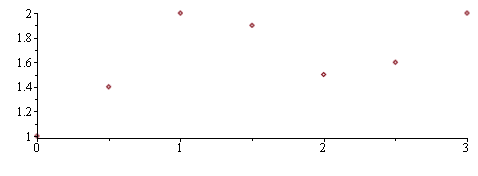
| > |
plot(data,style=point); |
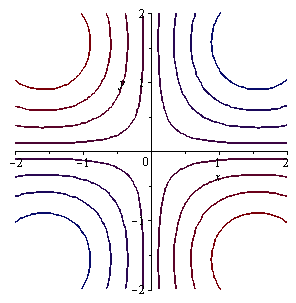
Vrstevnice funkce z=f(x,y)
Pozor tento prikaz je součáetí balíku programů plots
| > |
contourplot(sin(x)*sin(y),x=-2..2,y=-2..2); |
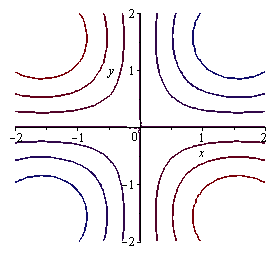
Volba vrstevnic.
| > |
contourplot(sin(x)*sin(y),x=-2..2,y=-2..2,contours=[-0.75,-0.5,-0.25,0,0.25,0.5,0.75]); |
Grafy 3D
Nejjednodušší vykreslení grafu.
| > |
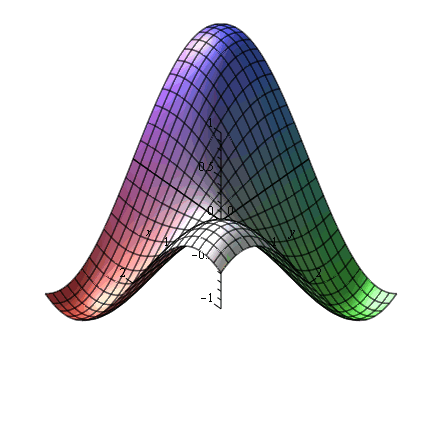
plot3d(sin(x)*sin(y),x=-2..2,y=-2..2); |
Teď použijeme různé volby (options).
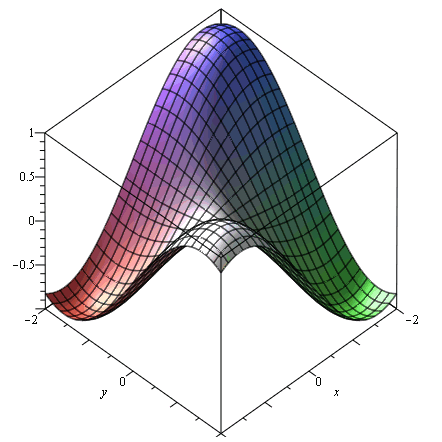
1. Přidáme box
| > |
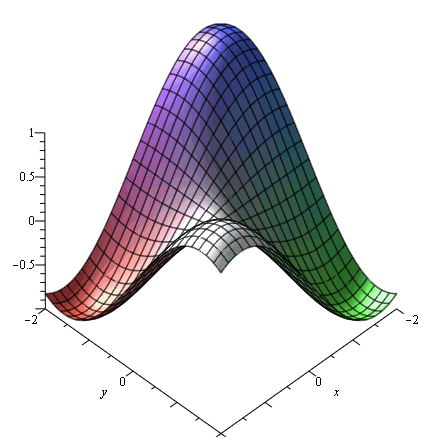
plot3d(sin(x)*sin(y),x=-2..2,y=-2..2,axes=boxed); |
2. Přidáme osy
| > |
plot3d(sin(x)*sin(y),x=-2..2,y=-2..2,axes=normal); |
| > |
plot3d(sin(x)*sin(y),x=-2..2,y=-2..2,axes=frame); |
3. změna sítě
| > |
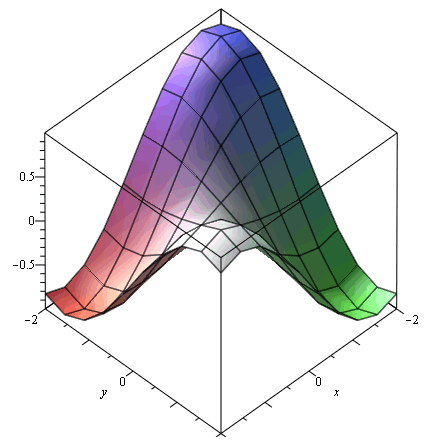
plot3d(sin(x)*sin(y),x=-2..2,y=-2..2,axes=boxed,grid=[10,10]); |
Parametrické grafy 3D
Parametricky zadaná křivka v R3
| > |
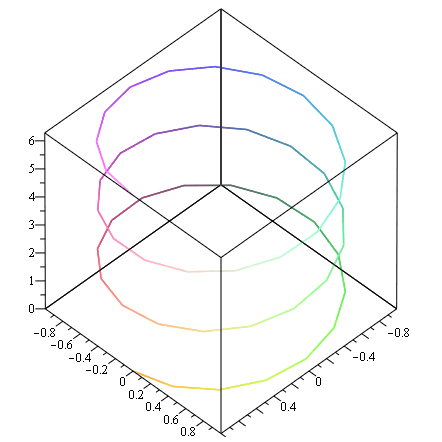
spacecurve([cos(t),sin(t),t/3],t=0..6*Pi,axes=boxed); |
Parametricky zadaná plocha
| > |
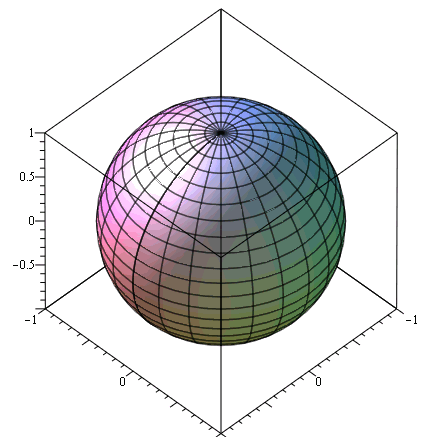
plot3d([cos(t)*sin(u),sin(t)*sin(u),cos(u)],t=0..2*Pi,u=0..Pi,axes=boxed); |
Numerická matematika
Vyčíslení výrazů, přesnost
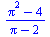 |
(6.1.1) |
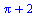 |
(6.1.2) |
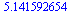 |
(6.1.3) |
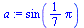 |
(6.1.4) |
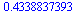 |
(6.1.5) |
implicitně je přesnost 10 platných míst, nastavíme ji na 16.
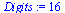 |
(6.1.6) |
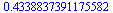 |
(6.1.7) |
vrátíme zase přesnost na 10 platných míst
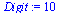 |
(6.1.8) |
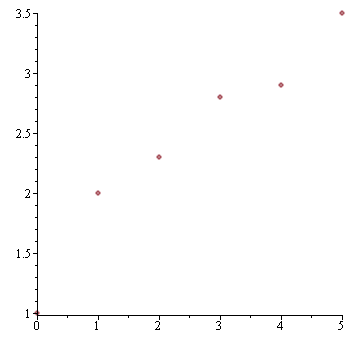
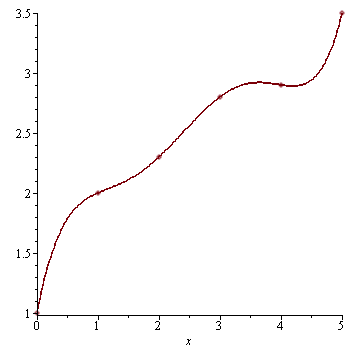
Metoda nejmenších čtverců
| > |
data:=[[0,1],[1,2],[2,2.3],[3,2.8],[4,2.9],[5,3.5]]; |
![[[0, 1], [1, 2], [2, 2.3], [3, 2.8], [4, 2.9], [5, 3.5]]](images/ManualMaple_158.gif) |
(6.2.1) |
| > |
plot(data,style=POINT); |
| > |
data1:=convert(linalg[col](data,1),list); |
![[0, 1, 2, 3, 4, 5]](images/ManualMaple_160.gif) |
(6.2.2) |
| > |
data2:=convert(linalg[col](data,2),list); |
![[1, 2, 2.3, 2.8, 2.9, 3.5]](images/ManualMaple_161.gif) |
(6.2.3) |
Proložení přímkou
| > |
r:=fit[leastsquare[[x,y]]]([data1,data2]); |
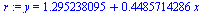 |
(6.2.4) |
| > |
fit[leastsquare[[x,y],y=a*x+b,{a,b}]]([data1,data2]); |
 |
(6.2.5) |
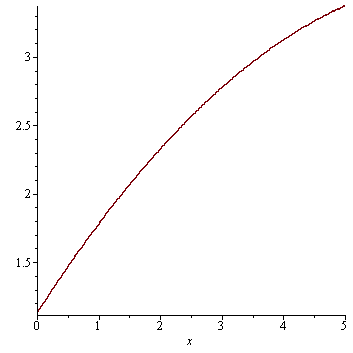
Proložení parabolou
| > |
r2:=fit[leastsquare[[x,y],y=a*x^2+b*x+c,{a,b,c}]]([data1,data2]); |
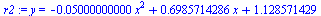 |
(6.2.6) |
Vykreslení do jednoho obrazku
| > |
g1:=plot(data,style=POINT): |
| > |
g2:=plot(rhs(r),x=0..5): |
| > |
g3:=plot(rhs(r2),x=0..5): |
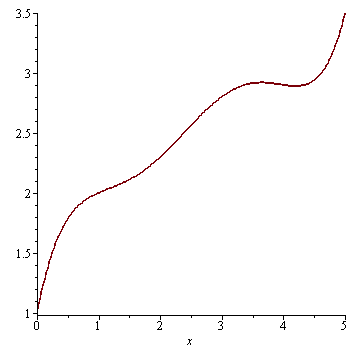
Interpolace
![[0, 1, 2, 3, 4, 5]](images/ManualMaple_168.gif) |
(6.3.1) |
![[1, 2, 2.3, 2.8, 2.9, 3.5]](images/ManualMaple_169.gif) |
(6.3.2) |
| > |
y:=interp(data1,data2,x); |

 |
(6.3.3) |
Rychlá Fourierova transformace
Musíme zavolat balík programů DiskreteTransforms
| > |
with(DiscreteTransforms); |
![[DiscreteWaveletTransform, FourierTransform, InverseDiscreteWaveletTransform, InverseFourierTransform, WaveletCoefficients, WaveletPlot]](images/ManualMaple_174.gif)
![[DiscreteWaveletTransform, FourierTransform, InverseDiscreteWaveletTransform, InverseFourierTransform, WaveletCoefficients, WaveletPlot]](images/ManualMaple_175.gif) |
(6.4.1) |
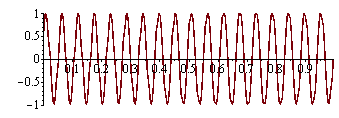
Vytvoření diskrétních dat
| > |
f:=i->sin(36*Pi*i/256); |
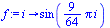 |
(6.4.2) |
 |
(6.4.3) |
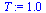 |
(6.4.4) |
| > |
data:=evalf(Vector(256,f)); |
](images/ManualMaple_179.gif) |
(6.4.5) |
Vykraslení diskrétních dat
| > |
pdata:=[seq([(i-1)*dt,evalf(f(i))],i=1..256)]: |
Rychlá Fourierova transformace
| > |
fdata:=FourierTransform(data); |
](images/ManualMaple_181.gif) |
(6.4.6) |
 |
(6.4.7) |
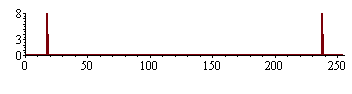
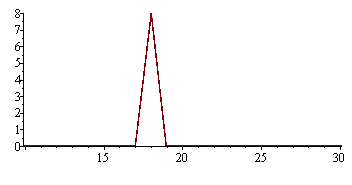
Vykreslení dat diskrétní Fourierovy transformace
| > |
pfdata:=[seq([dv*(i-1),abs(fdata[i])],i=1..256)]: |
Puvodní data mají frekvenci 18 Hz.
Numerická integrace
| > |
Int(x^x,x=0..1)=int(x^x,x=0..1); |
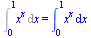 |
(6.5.1) |
Maple neumí vypočítat integrál analyticky, vypočteme ho pomocí numerické integrace
| > |
Int(x^x,x=0..1)=evalf(Int(x^x,x=0..1)); |
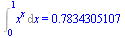 |
(6.5.2) |
Použití různých metod.
Počítáme s přesností 14 platných míst. 14 míst je přesnost počítače ne numerické metody
| > |
Int(x^x,x=0..1)=evalf[14](Int(x^x,x=0..1,method = _Gquad)); |
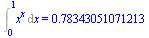 |
(6.5.3) |
| > |
Int(x^x,x=0..1)=evalf[14](Int(x^x,x=0..1,method = _NCrule)); |
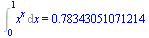 |
(6.5.4) |
| > |
Int(x^x,x=0..1)=evalf[14](Int(x^x,x=0..1,method = _d01ajc)); |
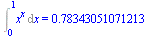 |
(6.5.5) |
Zkusíme teď příklad, pro který umíme určit přesné řešení.
Přesné řešení
| > |
Int(x^4,x=0..1)=int(x^4,x=0..2); |
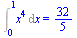 |
(6.5.6) |
 |
(6.5.7) |
Numerické řešení
| > |
vn:=evalf[30](Int(x^4,x=0..2,method = _Gquad)); |
 |
(6.5.8) |
| > |
vn:=evalf[30](Int(x^4,x=0..2,method = _NCrule)); |
 |
(6.5.9) |
Pokud Maple umí vypočítat přesné řešení, nikdy nepočíta numerické řešení (ať zvolíte jakoukoliv metodu) vždy vypočte přesné řešení a numericky ho vyjádří.
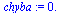 |
(6.5.10) |
Numerická suma, součin
Přesný výpočet sumy.
| > |
Sum(1/n^2,n=1..infinity)=sum(1/n^2,n=1..infinity); |
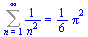 |
(6.6.1) |
Někdy Maple neumí přesný součet vypočítat.
| > |
Sum(1/(n^3+n!),n=1..infinity)=sum(1/(n^3+n!),n=1..infinity); |
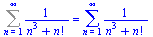 |
(6.6.2) |
Přibližný výpočet sumy.
| > |
Sum(1/(n^3+n!),n=1..infinity)=evalf(sum(1/(n^3+n!),n=1..infinity)); |
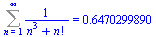 |
(6.6.3) |
Přesný výpočet součinu.
| > |
Product(1/n,n=1..10)=product(1/n,n=1..10); |
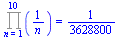 |
(6.6.4) |
Přibližné vvjádření výsledku.
| > |
Product(1/n,n=1..10)=evalf[30](product(1/n,n=1..10)); |
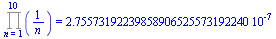 |
(6.6.5) |
Numerické řešení polynomiálních rovnic
| > |
evalf(solve(x^7+x+1=0,x)); |
Numerické řešení rovnic iterační metodou
Nutno zadat počáteční iteraci
 |
(6.8.1) |
Někdy má rovnice víc řešení
| > |
fsolve(3*sin(x)=x,x=0); |
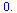 |
(6.8.2) |
| > |
fsolve(3*sin(x)=x,x=3); |
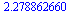 |
(6.8.3) |
| > |
fsolve(3*sin(x)=x,x=-3); |
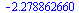 |
(6.8.4) |
Numerické řešení differenciálních rovnic
Numericky řešíme pouze partikulární řešení
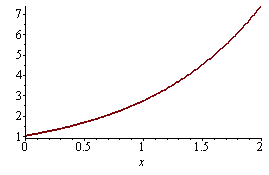
Nejdříve analytické řešení a jeho graf
| > |
 |
| > |
r:=dsolve({diff(y(x),x)=y(x),y(0)=1},y(x)); |
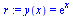 |
(6.9.1) |
Teď numerické řešení a jeho graf
| > |
rn:=dsolve({diff(y(x),x)=y(x),y(0)=1},y(x),numeric); |
 |
(6.9.2) |
| > |
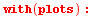 |
| > |
![odeplot(rn, [x, y(x)], x = 0 .. 2); 1](images/ManualMaple_216.gif) |
Příkaz odeplot nelze použít v Maple classic (při ukládání souboru Maple skončí chybou)
Ukázka použití některých voleb (options). Volba rozsahu pro nezávisle proměnnou
| > |
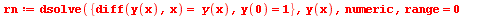
 |
 |
(6.9.3) |
| > |
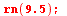 |
![[x = 9.5, y(x) = HFloat(13359.704400562758)]](images/ManualMaple_222.gif) |
(6.9.4) |
Volba metody
| > |
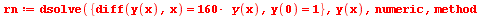
 |
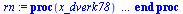 |
(6.9.5) |
| > |
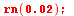 |
![[x = HFloat(0.02), y(x) = HFloat(24.532530196774943)]](images/ManualMaple_227.gif) |
(6.9.6) |
| > |
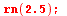 |
| Error, (in rn) cannot evaluate the solution past 0.72952958e-1, step size < hmin, problem may be singular or error tolerance may be too small |
|
Změna minimálního kroku (lze jen u některých metod)
| > |
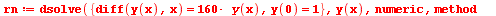
 |
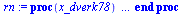 |
(6.9.7) |
| > |
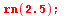 |
![[x = HFloat(2.5), y(x) = HFloat(5.221469679155235e173)]](images/ManualMaple_233.gif) |
(6.9.8) |
Porovnání numerické hodnoty a přesné hodnoty
| > |
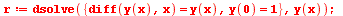 |
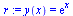 |
(6.9.9) |
| > |
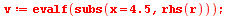 |
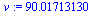 |
(6.9.10) |
| > |
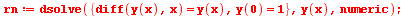 |
 |
(6.9.11) |
| > |
![vn := rhs(rn(4.5)[2]); 1](images/ManualMaple_240.gif) |
 |
(6.9.12) |
| > |
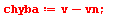 |
 |
(6.9.13) |
Numerické řešení soustavy diferenciálních rovnic, graf jednotlivých řešení
| > |
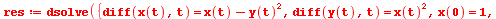
 |
 |
(6.9.14) |
| > |
![odeplot(res, [t, x(t)], 0 .. 1); 1](images/ManualMaple_247.gif) |
| > |
![odeplot(res, [t, y(t)], 0 .. 1); 1](images/ManualMaple_249.gif) |
Graf jednotlivých řešení do jednoho grafu
| > |
![odeplot(res, [[t, x(t)], [t, y(t)]], 0 .. 1); 1](images/ManualMaple_251.gif) |
Zobrazení trajektorie
| > |
![odeplot(res, [x(t), y(t)], 0 .. 1); 1](images/ManualMaple_253.gif) |
Optimalizace, lineární programování
![[ImportMPS, Interactive, LPSolve, LSSolve, Maximize, Minimize, NLPSolve, QPSolve]](images/ManualMaple_255.gif) |
(6.10.1) |
| > |
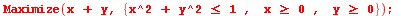 |
![[1.41421356237468987, [x = HFloat(0.7071067811873449), y = HFloat(0.7071067811873449)]]](images/ManualMaple_257.gif) |
(6.10.2) |
| > |
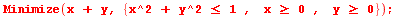 |
![[-0.444089209850062616e-15, [x = HFloat(-2.220446049250313e-16), y = HFloat(-2.220446049250313e-16)]]](images/ManualMaple_259.gif) |
(6.10.3) |
LPSolve minimizuje lineární finkci za určitých lineárních podmínek
| > |
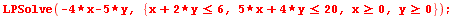 |
![[-19., [x = HFloat(2.6666666666666674), y = HFloat(1.6666666666666663)]]](images/ManualMaple_261.gif) |
(6.10.4) |
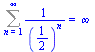
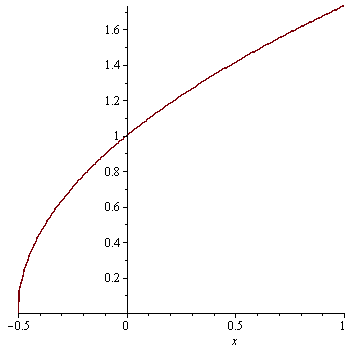
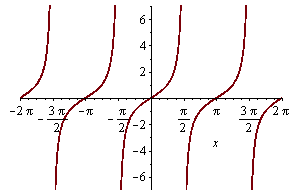
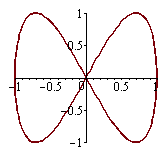
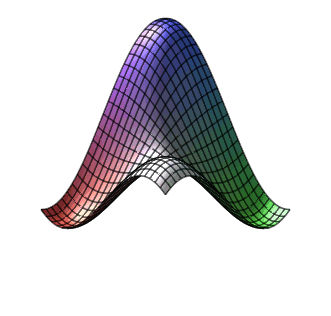
](images/ManualMaple_115.gif)

](images/ManualMaple_132.gif)
, Matrix(%id = 4678004930)](images/ManualMaple_133.gif)

](images/ManualMaple_141.gif)
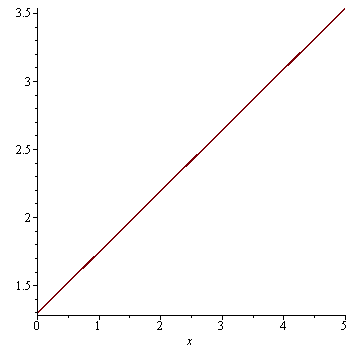
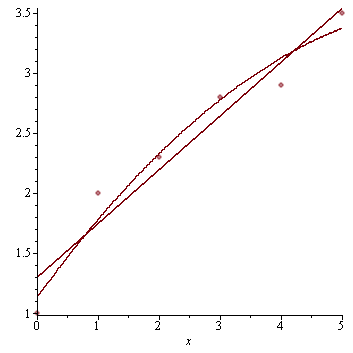
](images/ManualMaple_179.gif)
](images/ManualMaple_181.gif)