Mathematica 8
(stručný manuál)
Algebraické úpravy
Symbolické výpočty - algebraické úpravy
Expand - roznásobí mnohočleny a vrátí součet jednotlivých členů
Factor - napíše výraz jako násobení nejmenších faktorů
Simplify - zkusí najít nejjednodušší formu výrazu pomocí standardních alg. transformací
Podobně pro goniometrické výrazy TrigExpand, TrigFactor
Pro komplexní výrazy - ComplexExpand
Krácení zlomků
Rozklad na parciální zlomky
Rozklad na parciální zlomky vzhledem k x
Rozklad na parciální zlomky vzhledem k y
Symbolická matematika
Funkce
Tabulka elementárních finkcí:
Vlastní definice funkce f(x)
Vlastní definice funkce zadané po částech f(x)=
| |
|
Derivace
První derivace - f ' (x)
Třetí derivace - f '’’(x)
Parciální derivace podle x - 
(x,y)
Parciální derivace podle y - 
(x,y)
Diferenciál funkce f(x,y)
Diferenciál funkce f(x,y,a)
Integrace
Primitivní funkce k funkci f(x)
Jiný způsob zápisu - pomocí palety:
Primitivní funkci k funkci f(x) označím F(x)
Pozor !!! Mathematica obecně počítá v komplexním oboru, kde je definovaný logaritmus ze záporného čísla. Proto také předchozí výsledek není Log(|x|)
Určitý integrál z funkce f(x) od a do b
Jiný způsob zápisu - pomocí palety:
Nevlastní integrál:
1. Integrál diverguje
2. Integrál konverguje
Nevlastní integrál s parametrem:
Výsledek 
platí pouze pro Re(n) > -1 !!! Můžeme při výpočtu zadat podmínku pro parametr.
Někdy primitivní funkci Mathematica nevypočte (neznamená to, že neexistuje):
Suma
Součet nekonečné řady:
Součet nekonečné funkční řady:
Pozor !!!! Mathematica nám neřekne pro která x součet platí. V tomto případě to plati pro |x|>1. Například si můžeme ukázat, že pro 
nebo x = -1řada diverguje.
Limity
limita f(x) když x se blíží k a ( 
f(x) )
Mathematica počítá (pokud se jí to neupřesní) limitu zprava, proto ten výsledek ∞
Dotážem se na volby (options) příkazu Limit
Použijem některé volby
limita f(x) když x se blíží k a zprava ( 
f(x) )
limita f(x) když x se blíží k a zleva ( 
f(x) )
Grafy
Grafy 2D
Nejjednodušší vykreslení grafu.
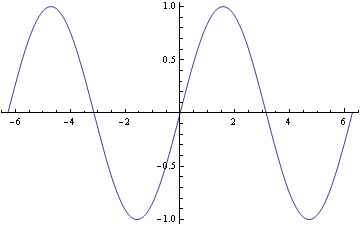
Teď použijeme různé volby (options).
1. Rozsah osy y
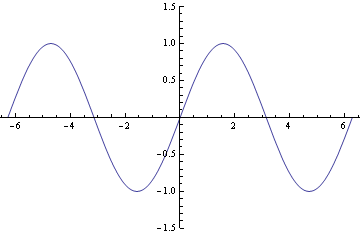
2. Číselný popis osy x a y
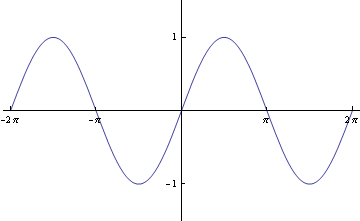
3. Poměr osy y ku ose x
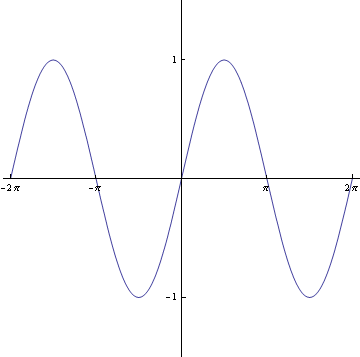
4. Popis os
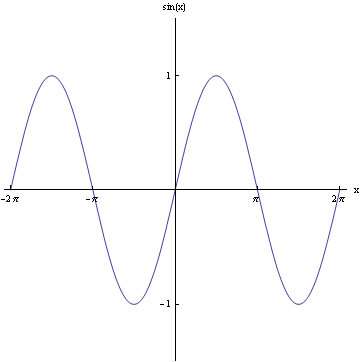
5. Vykreslení dvou grafů do jednoho souřadnicového systému a zároveň použití definování tlouštky a barvy grafu
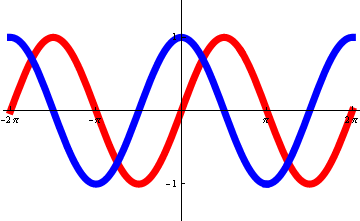
6. Barva pozadí (šedá, barevná)
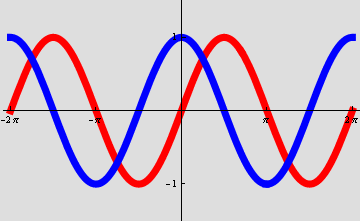
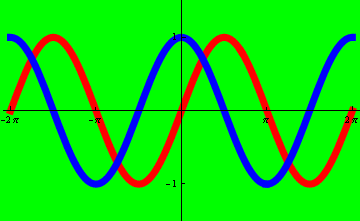
7. Sestavení matice grafů
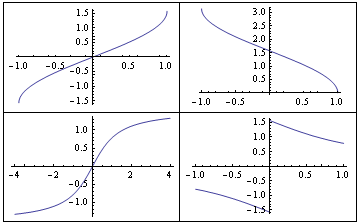
8. Pozor na grafy, které nejsou definované na celém R
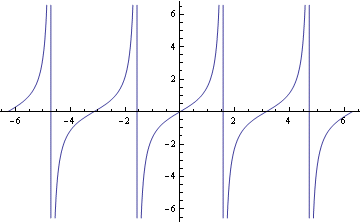
Vyloučíme body, kde Tangents není definován
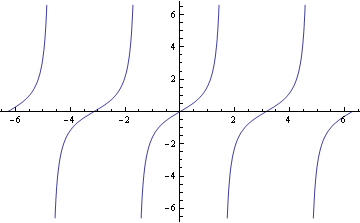
Můžeme přidat asymptody
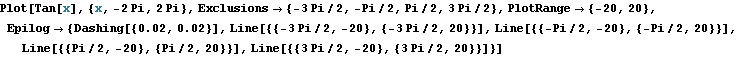
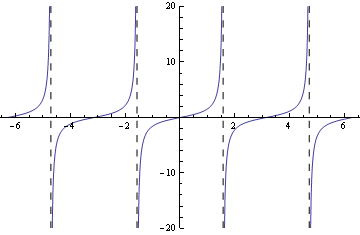
Parametrické grafy 2D
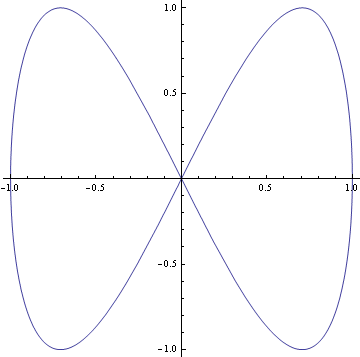
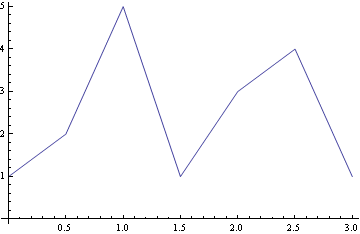
List grafy 2D
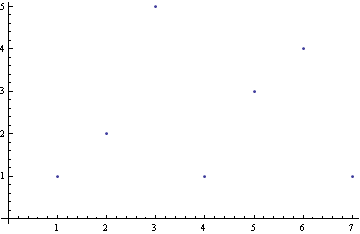
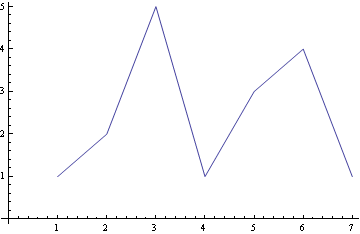
Vrstevnice funkce z=f(x,y)
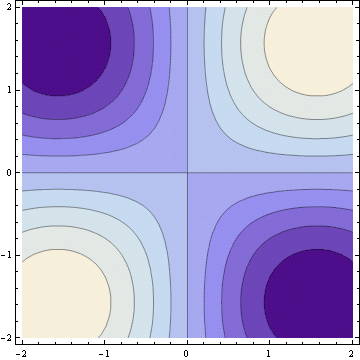
Pomocí voleb mohu ovlivnit vybarvení, počet vrstevnic nebo mohu zadat přímo určité vrstevnice
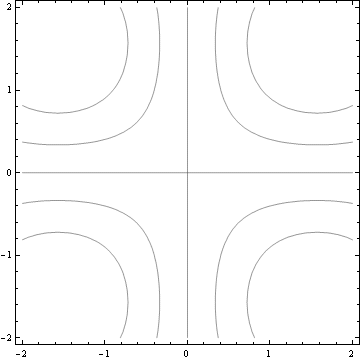
Vrstevnice z=0
Vrstevnice z=0.5
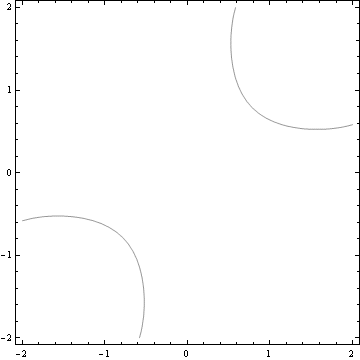
Vrstevnice z=-0.5
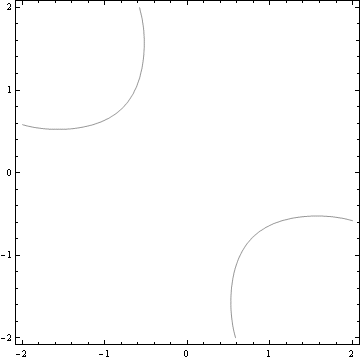
Vrstevnice z=-0.5, 0, 0.5
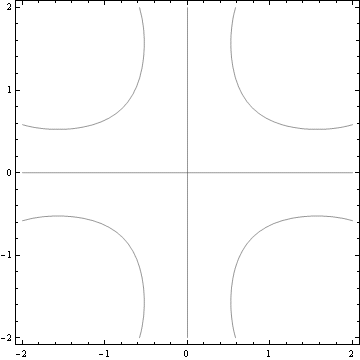
Graf 3D
Nejjednodušší vykreslení grafu.
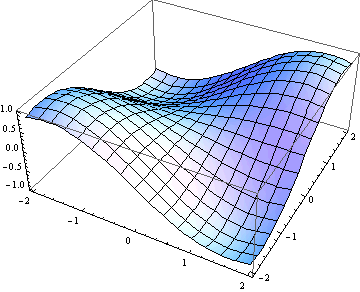
Teď použijeme různé volby (options).
1. Bod pohledu
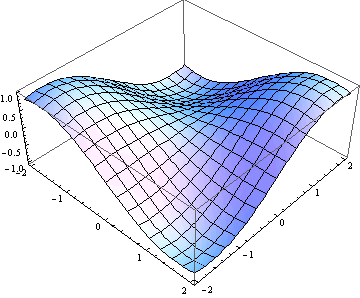
2. Poměr stran boxu
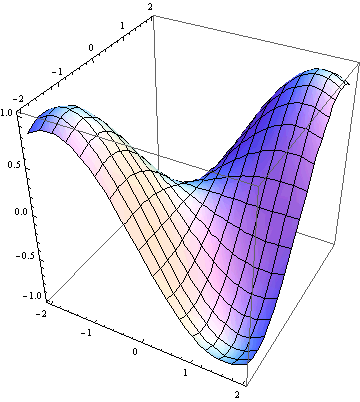
3. Graf bez mřížky
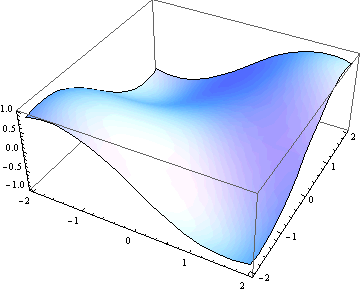
1. Pouze mřížka
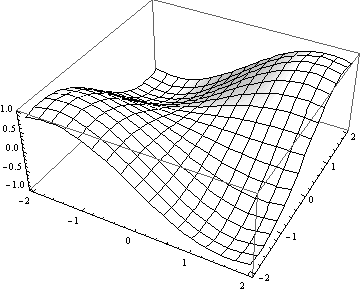
Parametrické grafy 3D
Parametricky zadaná křivka v 
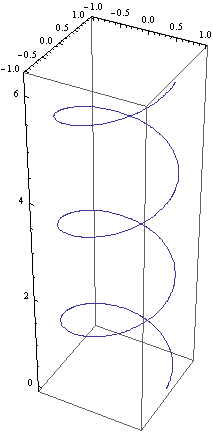
Parametricky zadaná plocha v 
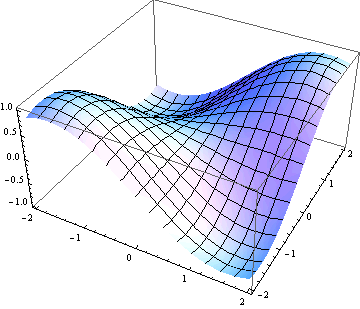
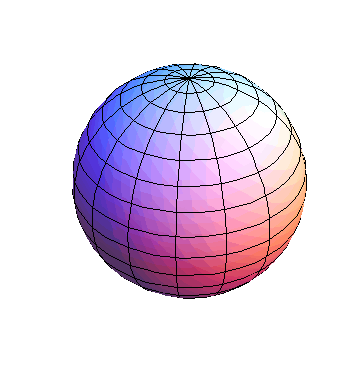
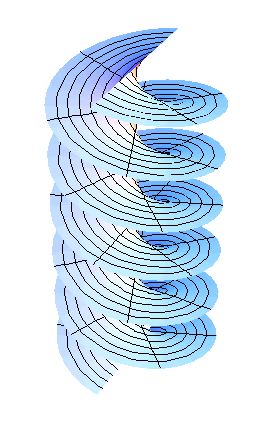
Řešení rovnic
Řešení alg. rovnic
Numerické vyřešení kořenů polynomu
Musíme použít příkaz FindRoot.
Příkaz FindRoot používá iterační metoda, která najde pouze jeden kořen. Musíte zvolit počáteční iteraci (zde 
=1).
Použití FindRoot má-li rovnice více kořenů.
Pomocí grafu a jednoduché úvahy se přesvedčíme, že jsme našli všechny kořeny
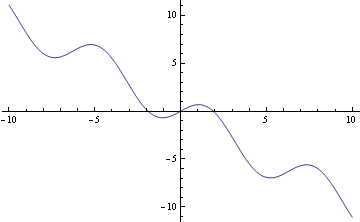
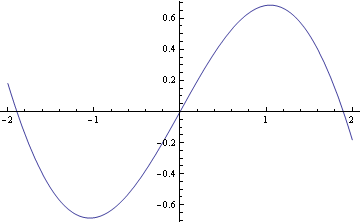
Řešení diferenciálních rovnic
Obecné řešení
Partikulární řešení splňující počáteční podmínku
Obecné řešení
Partikulární řešení splňující počáteční podmínku
Mathematica upozorňuje, že řešení je definované na otevřeném intervalu ( -0.5 ; ∞ )
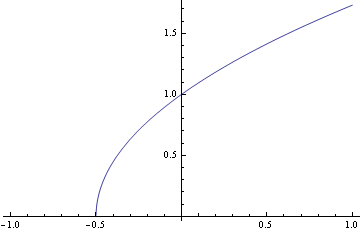
Obecné řešení soustavy rovnic
Partikulární řešení splňující počáteční podmínku
Nakreslení integrální křivky (graf partikulárního řešení x(t))
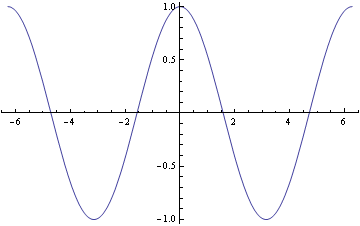
Nakreslení integrální křivky (graf partikulárního řešení y(t))
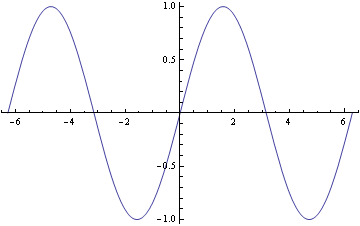
Nakreslení integrálních křivek do jednoho obrázku
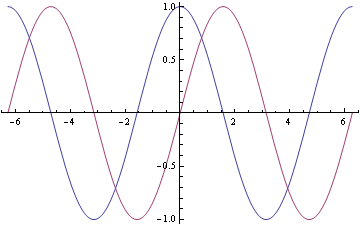
Nakreslení trajektorie řešení (graf parametricky zadané křivky)
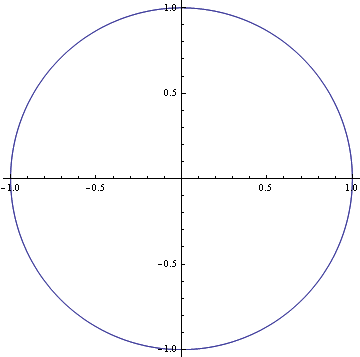
Obecné řešení
Určení partikulárního řešení volbou konstanty
Obecné řešení diferenciální rovnice vyššího řádu
Partikulární řešení splňující okrajové podmínky
Obecné řešení diferenciální rovnice vyššího řádu
Partikulární řešení splňující okrajové podmínky
Někdy partikulární řešení splňující okrajové podmínky neexistuje
Někdy existuje nekonečně řešení
Lineární algebra
Práce s vektory a maticemy
List je uspořádaná množina objektů {
,
, ..., 
}. Vektor i matice jsou listy.
Vektor
Matice
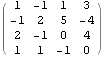
Násobení řádku matice příslušným prvkem vektoru
Násobení matice a vektor
Násobení matice maticí
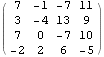
Napojování matic
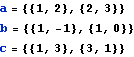
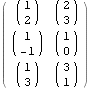
Zápis matice pomocí palety
Vyrobení matice pomocí příkazu table (pomocí předpisu)
i-tý řádek matice
Prvek i,j matice
Transponovaná matice
Inverzní matice
Mathematica nás upozornila, že matice T je singulární
Vlastní čísla matice A
Vlastní vektory matice A
Mathematica nám vrátí vlastní čísla (první složka) a vlastní vektory (druhá složka)
Determinant matica A
Přidání řádku k matici na začátek matice
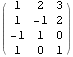
Přidání řádku k matici na konec matice
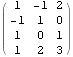
Připojení řádku k matici na začátek i konec matice
Jakobiho matice
Vymazání proměnných a,b,c
Využití příkazu outer k vytvoření Jakobiho matice
Jakobiho matice k zobrazení 
(r,t)=(r cos(t),r sin(t))
Příkaz Map
Příkaz Map
Rozklady matic
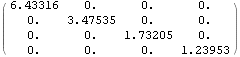
Singulární rozklad
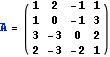
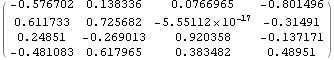
QR rozklad
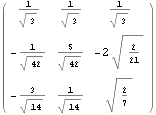
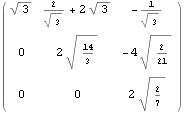
Jordánův rozklad
Manipulate
Numerická matematika
Vyčíslení výrazů, přesnost
Metoda nejmenších čtverců
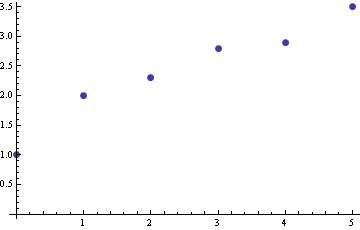
Proložení přímkou
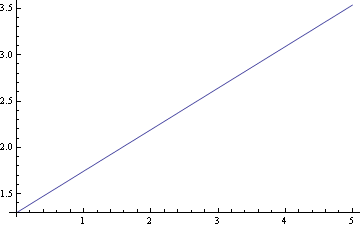
Proložení parabolou
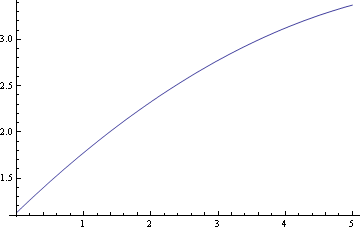
Vykreslení do jednoho obrázku
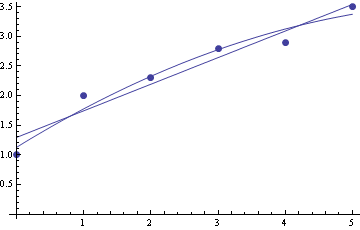
Interpolace
Interpolační polynom
Vykreslení interpolačního polynomu
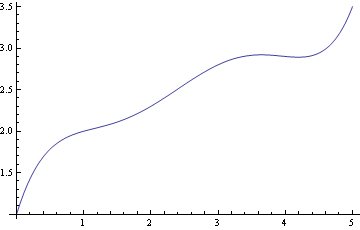
Vykreslení interpolačního polynomu a interpolavaných dat do jednoho obrázku
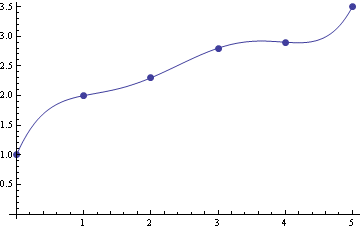
Rychlá Fourierova transformace
Vytvoření diskrétních dat
Vykreslení diskrétních dat
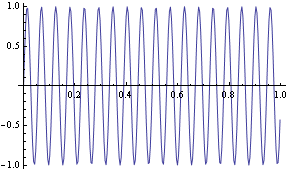
Rychlá Fourierova transformace
Vykreslení dat diskrétní Fourierovy transformace
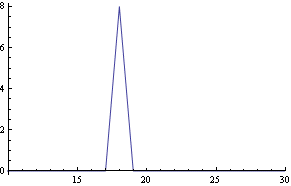
Numerická integrace
Mathematica neumí vypočítat integrál analyticky, vypočteme ho pomocí numerické integrace
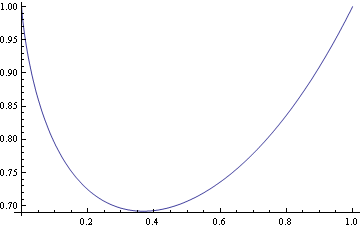
Použití různých voleb k numerické integraci
Na kolik míst je výpočet správný
Použití různých metod numerické integrace.
Přesnost počítače ( není to přesnost numerické metody)
Přesné řešení
Chyba numerického řešení
Numerická suma, součin
Přesný výpočet sumy.
Někdy Mathematica neumí přesný součet vypočítat.
Přibližný výpočet sumy.
Přesný výpočet součinu.
Přibližné vvjádření výsledku.
Numerické řešení polynomiálních rovnic
Numerické řešení rovnic iterační metodou
Nutno zadat počáteční iteraci
Někdy má rovnice víc řešení
Numerické řešení differenciálních rovnic
Numericky řešíme pouze partikulární řešení
Nejdříve analytické řešení a jeho graf
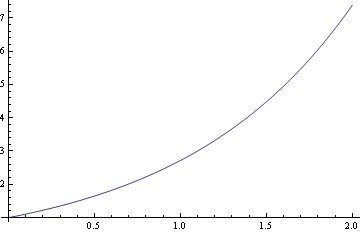
Teď numerické řešení a jeho graf
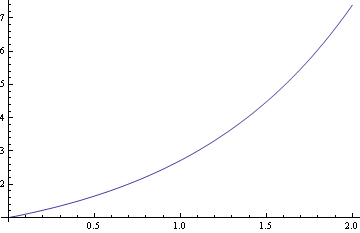
Numerické řešení je vhodné použít, jen když neumíme vypočítat řešení analiticky
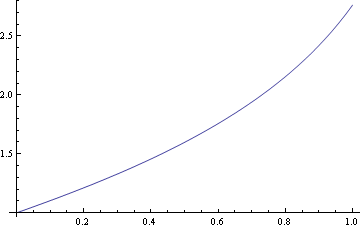
Ukázka použití některých voleb (options)
Různé metody integrace:
Počet kroků integrace (implicitně je počet kroků 10 000):
Je lepší použít jinou metodu integrace
Porovnání numerické hodnoty a přesné hodnoty
Numerické řešení soustavy diferenciálních rovnic, graf jednotlivých řešení
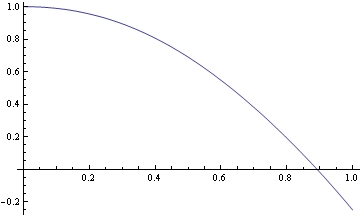
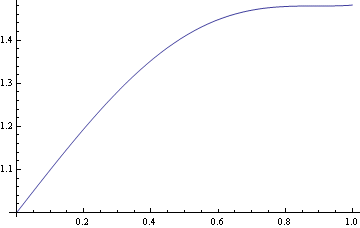
Graf jednotlivých řešení do jednoho grafu
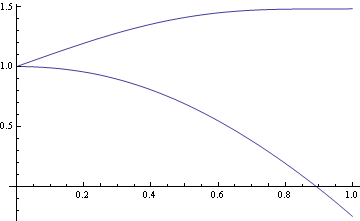
Zobrazení trajektorie
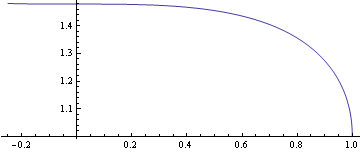
Numerické nalezení minima a maxima (iterační metoda)
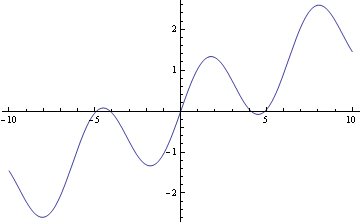
Optimalizace
Numerický výpočet maxima
Numerický výpočet minima
Pokud Maximize nevypočte maximum analyticky musíme použít NMaximize (podobně Minimize)
