|

|
E-tabulky
|


|
Návod
k popisu rovnováhy kapalina-pára rovnicemi
Jak víte z fyzikální chemie, korektní postup při analytickém popisu
fázových rovnováh vychází z toho, že fugacita každé ze složek musí být v
rovnovážných fázích stejná. Má-li být tento přístup používán s vynaložením
rozumného úsilí, je třeba mít k dispozici sadu hotových podprogramů pro takové
výpočty. Protože je zatím nemáme, používají se na cvičeních zjednodušené
postupy, které vycházejí z pojmu relativní těkavosti. Relativní těkavost je
definována pro binární směs obsahující těkavější složku A a méně těkavou složku
B vztahem
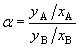 (1) (1)
kde x je
molární zlomek příslušné složky v kapalné fázi a y totéž v parní. (Všechny
v tomto návodu uvedené vztahy platí jak pro molární, tak pro hmotnostní zlomky,
stačí zaměnit x za w a y
za u.) Z rovnice (1) plyne
pro binár (kde platí xA + xB = 1, yA + yB = 1) rovnovážná
závislost ve tvaru
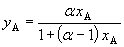 (2) (2)
Pokud
lze v rozsahu koncentrací, pro který je třeba při řešení úlohy znát rovnovážnou
závislost, považovat relativní těkavost za konstantní, je vše hotovo. Pokud se a mění jen málo, dosadíme do rovnice (2) vhodnou střední hodnotu. Ze
zkušenosti je známo, že při diferenciální destilaci je to
a =
(a W a F)0,5 (3)
Stejně
můžeme postupovat i při rovnovážné destilaci, tam ovšem složení zbytku většinou
neznáme a musíme ho odhadnout. Při rektifikaci počítáme střední hodnotu a ze vztahu
a =
(a W a F a D)(1/3) (4)
kde a W, a F a a D jsou
relativní těkavosti vypočtené z tabulky rovnováhy z rovnice (1) pro složení
kapaliny co nejbližší složení zbytku xW,
nástřiku xF a destilátu xD jaké se dá v tabulce
najít. Mění-li se relativní těkavost značně se složením, je třeba ji vypočíst
pro všechny body rovnováhy v potřebném intervalu koncentrací a nalézt její závislost na složení kapaliny,
například regresí v Excelu. (Často stačí polynom druhého stupně, nemá smysl
používat polynom vyššího stupně než třetího).
Pro velmi neideální
směsi nevyhovuje ani tento postup, téměř vždy se podaří rovnováhu popsat
vztahem
yA = Pm (xA) / Pn (xA) (5)
kde Pm (xA) a Pn (xA) jsou polynomy m-tého
a n-tého stupně. V literatuře [1,2] se uvádějí důvody, proč je vhodné používat pouze níže uvedené kombinace
hodnot m a n. Rovnice (6) až (8)
jsou upraveny tak, aby pro xA = 0
vycházelo yA = 0
a pro xA = 1
yA = 1.
m = n = 2
yA = xA(a xA + b)/(
xA2 + c
xA + d) (6)
kde d = a +b - c - 1
m = 2, n = 3
yA = xA(a xA + b)/(
xA3 + c
xA2 + d xA + e) (7)
kde e = a +b - c - d - 1
m = n = 3
yA = xA(a xA2 + b xA + c)/(
xA3 + d
xA2 + e xA + f) (8)
kde f = a +b + c - d - e - 1
Veličiny a,b,c,d,e jsou
empirické konstanty, které je třeba vyhodnotit nelineární regresí z dat v
tabulce příslušné rovnováhy. Ze software, který máte k dispozici, lze jednoduše
provést nelineární regresi pouze v programu Polymath.
Příklady
Příklad 1
Pro výpočet rovnovážné
destilace směsi n-heptan - n-oktan chceme popsat rovnovážnou závislost pro
případ, kdy odhadnutý hmotnostní zlomek heptanu ve zbytku wW = 0,2
a v nástřiku wF = 0,4.
Protože jde o téměř ideální směs, použijeme rovnici (2) a budeme předpokládat,
že střední relativní těkavost vypočtená z rovnice (3) je v uvedeném rozsahu
koncentrací konstantní a platnost předpokladu ověříme porovnáním vypočtených
hodnot koncentrace heptanu v páře s experimentálními. Z příslušné e-tabulky
máme
|
w
|
u
|
|
0,20
|
0,3692
|
|
0,40
|
0,6095
|
Ze vztahu (1) vypočteme
a W = (0,3692 / 0,2)
/ [(1-0,3692) / (1-0,2)] = 2,34115
a F = (0,6095/ 0,4) /
[(1-0,6095) / (1-0,4)] = 2,34123
Z rovnice
(3) máme
a =
(2,34115. 2,34123)0,5 = 2,3412
Porovnání experimentálních hodnot hmotnostních zlomků heptanu v páře s
hodnotami vypočtenými z rovnice (2) pro a = 2,3412 je v následující tabulce:
|
w
|
u experimentální
|
u vypočtené
|
|
0,20
|
0,3692
|
0,3692
|
|
0,25
|
0,4382
|
0,4383
|
|
0,30
|
0,5006
|
0,5008
|
|
0,35
|
0,5575
|
0,5576
|
|
0,40
|
0,6095
|
0,6095
|
Je vidět, že pro tento typ směsi a malý rozsah koncentrací je aproximace
rovnováhy rovnicí (2) s konstantní hodnotou a
určenou ze vztahu (3) zcela uspokojivá.
Příklad 2
V řešené úloze na diferenciální
destilaci v návodech na MAPLE se zpracovává diferenciální destilací směs
ethanol-voda s hmotnostním zlomku ethanolu wF = 0,33
tak, aby se získal destilát o hmotnostním zlomku ethanolu 0,65. V tomto případě
neznáme koncentraci zbytku wW a
chceme-li použít k výpočtu střední relativní těkavost vypočtenou podle
(3), musíme-ji odhadnout.Odhadneme-li wW = 0,1,
najdeme v e-tabulce rovnováhy
ethanol-voda
|
w
|
u
|
|
0,10
|
0,5386
|
|
0,35
|
0,7295
|
(pro
hmotnostní zlomek ethanolu v kapalině 0,33 v tabulce údaje nejsou, nejbližší
hodnota je 0,35). Odtud podle (1)
a W = (0,5386 / 0,1)
/ [(1-05386) / (1-0,1)] = 10,50585
a F = (0,7295/ 0,35) /
[(1-0,7295) / (1-0,35)] = 5,00845
Z rovnice (3) máme
a =
(10,50585 . 5,00845 )0,5 = 7,25383
Pro tuto směs a závisí značně na koncentraci
těkavější složky v kapalině, porovnáme-li koncentrace v páře vypočtené z
rovnice (2) pro a =
7,25383 z hodnotami z
e-tabulek, dostaneme
Porovnání
experimentální rovnováhy ethanol-voda s výpočtem
za předpokladu
konstantní relativní těkavosti
|
w
|
u experimentální
|
u vypočtené
|
|
0,10
|
0,5386
|
0,4463
|
|
0,15
|
0,6128
|
0,5614
|
|
0,20
|
0,6579
|
0,6446
|
|
0,25
|
0,6887
|
0,7074
|
|
0,30
|
0,7114
|
0,7566
|
|
0,35
|
0,7295
|
0,7962
|
Je vidět, že rovnováha je aproximována velmi
nepřesně. Vypočteme-li relativní těkavosti pro všechny body rovnováhy
ethanol-voda v intervalu w = 0,05 až 0,35, dostaneme kvadratickou regresí v
EXCELu vztah pro její závislost na hmotnostním zlomku ethanolu v kapalině
a =
43.914 w 2 - 41.761 w +
14.288 (A)
Počítáme-li
rovnovážné složení v páře z rovnice (2) a používáme přitom a
zjištěné z rovnice (A), dostaneme následující tabulku
Porovnání
experimentální rovnováhy ethanol-voda s výpočtem
za předpokladu
platnosti rovnice (A)
|
w
|
u experimentální
|
u vypočtené
|
|
0,05
|
0,3940
|
0,3932
|
|
0,10
|
0,5386
|
0,5397
|
|
0,15
|
0,6128
|
0,6139
|
|
0,20
|
0,6579
|
0,6579
|
|
0,25
|
0,6887
|
0,6873
|
|
0,30
|
0,7114
|
0,7100
|
|
0,35
|
0,7295
|
0,7312
|
Tímto
postupem je v potřebném rozsahu koncentrací rovnováha aproximována uspokojivě.
Příklad 3
Pro výpočet
rektifikační kolony je třeba aproximovat rovnováhu ethanol-voda v rozsahu
molárního zlomku ethanolu v kapalině x =
0,01 až 0,9. Můžete si sami vyzkoušet, že postupem použitým v příkladu 2 se to
nepodaří, ani když vyjádříte závislost relativní těkavosti na molárním
zlomku ethanolu v kapalině polynomem třetího stupně. Nelineární regresí v
programu POLYMATH dostaneme pro rovnici (8) konstanty
a = 0,220093 ; b = -0,85931;
c = -0,18148; d = -1,4744;
e = -0,33385; f = -0,01245
Porovnáme-li hodnoty molárních zlomků ethanolu v páře
vypočtené z rovnice (8) s hodnotami z příslušné e-tabulky, dostaneme
následující výsledky (chyba je rozdíl vypočtené a experimentální hodnoty)
|
x
|
y experimentální
|
y vypočtené z (8)
|
chyba
|
|
0,000
|
0,0000
|
0
|
0,0000
|
|
0,010
|
0,1191
|
0,1193
|
0,0002
|
|
0,030
|
0,2616
|
0,2614
|
-0,0002
|
|
0,050
|
0,3425
|
0,3423
|
-0,0002
|
|
0,100
|
0,4451
|
0,4452
|
0,0001
|
|
0,150
|
0,4961
|
0,4962
|
0,0001
|
|
0,200
|
0,5292
|
0,5293
|
0,0001
|
|
0,250
|
0,5546
|
0,5546
|
0,0000
|
|
0,300
|
0,5765
|
0,5765
|
0,0000
|
|
0,350
|
0,5969
|
0,5967
|
-0,0002
|
|
0,400
|
0,6167
|
0,6165
|
-0,0002
|
|
0,450
|
0,6368
|
0,6366
|
-0,0002
|
|
0,500
|
0,6575
|
0,6574
|
-0,0001
|
|
0,550
|
0,6793
|
0,6793
|
0,0000
|
|
0,600
|
0,7027
|
0,7027
|
0,0000
|
|
0,650
|
0,7278
|
0,7279
|
0,0001
|
|
0,700
|
0,7552
|
0,7554
|
0,0002
|
|
0,750
|
0,7853
|
0,7856
|
0,0003
|
|
0,800
|
0,8186
|
0,8190
|
0,0004
|
|
0,850
|
0,8559
|
0,8563
|
0,0004
|
|
0,900
|
0,8978
|
0,8982
|
0,0004
|
|
0,904
|
0,9040
|
0,9017
|
-0,0023
|
|
0,950
|
0,9454
|
0,9456
|
0,0002
|
|
0,970
|
0,9663
|
0,9665
|
0,0002
|
|
0,990
|
0,9885
|
0,9885
|
0,0000
|
|
1,000
|
1,0000
|
1,0000
|
0,0000
|
Z
tabulky je vidět, že aproximace rovnováhy rovnicí (8) je dosti přesná.
Literatura
[1] William H. Press et al.: Numerical
Recipes in FORTRAN 77,Cambridge University Press 1993
[2] Anthony Ralston: Základy numerické matematiky, Academia Praha 1973
Poznámka
Při výpočtech na
cvičení a při testech samozřejmě nemusíte ověřovat vhodnost aproximace
rovnováhy porovnáním vypočtených koncentrací v páře s experimentálními. To za
Vás musí udělat učitel, dříve než Vám nějaký postup výpočtu doporučí. Při
výpočtech v praxi, kde jde o peníze, je ovšem takový postup nutný.
|
|