Absorpce v plněné koloně

Zadání 
Z plynné směsi obsahující 15% objemových amoniaku (zbytek inertní plyn nerozpustný ve vodě) je třeba odstranit 92% amoniaku absorpcí do čisté vody při teplotě 10°C. Vystupující roztok má obsahovat 15% hmotnostních amoniaku ve vodě. Absorpce se provádí v protiproudé koloně plněné keramickými Raschigovými kroužky o průměru 50 mm, tlak v koloně je 10⁵ Pa. Koeficient prostupu hmoty K_Y = 0,6 kmol m^-2h^-1. Objemový tok plynné směsi na vstupu do kolony je 1200 m³h^-1 (měřeno při 0°C a tlaku 101,3 kPa). Vypočtěte spotřebu čisté vody v kgh^-1, průměr kolony a potřebnou výšku výplně, můžete-li předpokládat, že mimovrstvová rychlost plynu v patě kolony je 0,55 ms^-1 a výplň je smočena ze 65%. 

Zadaná data:
složka A - amoniak            složka B - inertní plyn            složka C - voda 
y_i = 0,15; q = 0,92; x_i = 0; d_p = 50 mm; t = 10°C; p = 10⁵ Pa; K_Y = 0,6 kmol m^-2h^-1; 
u_f = 0,55 m s^-1; t₀ = 0°C; p₀ = 101,3 kPa; a/a_t = 0,65 

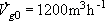
Řešení
Úlohu je možné řešit v hmotnostním i látkovém vyjádření, budeme počítat v látkových jednotkách. Nejprve vypočteme celkový látkový tok plynné směsi ze stavové rovnice ideálního plynu 

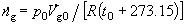(A)

Látkový tok inertního plynu spočteme ze vztahu 

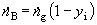(B)

Dále určíme relativní molární zlomek amoniaku v plynu na vstupu podle vztahu 

Yi = yi /(1 - yi)

(C)

a na výstupu z rovnice 

Ye = (1 - q) Yi

(D)

Zadaný hmotnostní zlomek amoniaku ve vystupujícím roztoku we přepočteme na relativní molární podle vztahu   Xe = (we/MA)/[(1- we )/ MC] (E) kde MA a MC jsou molární hmotnosti amoniaku a vody.  Z bilance kolony (viz schéma) vypočteme látkový tok čisté vody    (F) a přepočteme na hmotnostní tok násobením molární hmotností vody. Zadaný objemový tok plynné směsi na vstupu přepočteme z podmínek při kterých byl naměřen na podmínky v koloně podle vztahu   (G) Potřebný průřez kolony S vypočteme ze vztahu   (H) Z průřezu vypočteme průměr kolony   d = (4S/p)0,5 (I) Potřebnou výšku výplně h zjistíme jako součin výšky převodové jednotky HY a počtu převodových jednotek NY.   (J) kde veličina a je hustota povrchu smočené výplně, kterou zjistíme tak, že geometrickou hustotu povrchu výplně at , kterou najdeme pro zadaný druh a velikost výplně například ve sbírce příkladů z chemického inženýrství násobíme známým poměrem a/at (v tomto příkladu je zadán).

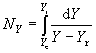(K)

kde Y je koncentrace absorbované látky v plynné fázi v tom místě kolony, kde její koncentrace v kapalné fázi je X a Y_r je koncentrace v plynu, který je v rovnováze s kapalinou o složení X. Rovnovážnou závislost najdeme pro směs amoniak-voda v e-tabulkách v podobě tabulky závislosti rovnovážného parciálního tlaku amoniaku p_A v plynu nad kapalinou o relativním hmotnostním zlomku amoniaku W. Protože úlohu řešíme v látkových jednotkách, musíme tyto údaje přepočítat na relativní molární zlomky. Uděláme to podle vztahů 

X = W MC /MA

(L)

a 

Yr = pA/(p - pA)

(M)

Závislost Y_r na X se dá polynomickou regresí v EXCELu vyjádřit ve tvaru

Yr = 4,5086X3 + 0,4187X2 + 0,467X

(N)

Abychom mohli spočítat integrál v rovnici (K), musíme všechny proměnné veličiny vyjádřit jako funkci jediné integrační proměnné. Protože Y_r už máme vyjádřeno jako funkci X, je nejjednodušší učinit totéž i s veličinou Y. Zapíšeme-li bilanci mezi místem v koloně, kde složení kapaliny a plynu je X a Y a horním koncem kolony (viz schéma), dostaneme z ní po úpravě

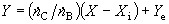(O)

a

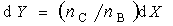(P)

a počet převodových jednotek N_Y pak vypočteme ze vztahu

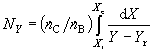(Q)

který získáme z rovnice (K). Rovnice (O) a (N) je třeba v programu napsat před rovnici (Q), aby MAPLE mohl za Y a Y_r před integrací dosadit. 

Zdrojový text