Čerpadlo

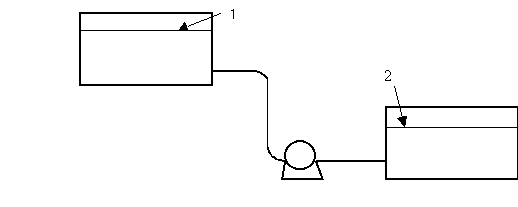
Zadání

Z železniční cisterny se při teplotě 20°C přemisťuje amylalkohol do podzemní nádrže ocelovým, mírně korodovaným potrubím dlouhým 48 m (včetně zabudovaných ekvivalentních délek armatur), vnitřního průměru 44 mm. Během vyprazdňování je v cisterně udržován konstantní tlak 96,5 kPa a v podzemní nádrži tlak 110,5 kPa. Vypočítejte, za jak dlouho se vyprázdní cisterna, která obsahuje 14 m³ amylalkoholu při použití odstředivého čerpadla, jehož charakteristika je zadána .
Při výpočtu pro zjednodušení předpokládejte, že svislá vzdálenost mezi hladinou v podzemní nádrži a hladinou v cisterně, která je 6 m, se během vyprazdňování cisterny nemění.
 

V[ls-1]	0	2	4	6	8	10
Hc[m]	22	22,4	22,6	22,4	21,5	20

l = 48 m
d = 44 mm = 0,044m
p₁ = 96,5 kPa = 96500 Pa
p₂ = 110,5 kPa = 110500 Pa
V = 14 m³
h₁ = 6 m
h₂ = 0 m

Řešení:

Pro potrubí, v němž je zařazeno čerpadlo, platí Bernoulliho rovnice mezi průřezy 1 a 2 zapsaná ve tvaru

p₁ / r+ / 2 + h₁ g + e_c = p₂ / r +  / 2 + h₂ g + e_dis1,2        (A)

Kapalina se čerpá ve směru od průřezu 1 k průřezu 2, p₁, p₂ jsou v tomto případě tlaky nad hladinami nádrží, u₁, u₂ jsou rychlosti hladin, které jsou rovny 0, g tíhové zrychlení a r hustota kapaliny. Člen e_c je energie, kterou čerpadlo předá jednotce hmotnosti čerpané kapaliny při průchodu čerpadlem a člen e_dis1,2 je měrná ztrátová energie mezi průřezy 1 a 2.

Místo e_c zavedeme pracovní výšku čerpadla  dle vztahu
 

= ec / g

(B)

Člen e_dis1,2 je měrná ztrátová energie mezi průřezy 1 a 2, kterou vypočítáme ze vztahu 
 

(C)

kde l je součinitel tření , l délka potrubí, d jeho průměr a u rychlost v potrubí.
 

u = / S

(D)

 

je objemový tok a S je průřez potrubí. 

Výpočet součinitele tření lzávisí na hodnotě Reynoldsova kritéria Re , které je pro trubku kruhového průřezu definováno vztahem
 

Re = u d r / h

(E)

kde r je hustota vody a hjejí dynamická viskozita, jejichž hodnotu pro danou teplotu nalezneme v tabulkách.

Bernoulliho rovnice po úpravě má tvar
 

= (p2 - p1 ) / r g - h1 + edis1,2/ g

(F)

Tím máme Bernoulliho rovnici ve tvaru, který se nazývá charakteristika potrubí. K němu potřebujeme získat charakteristiku čerpadla z údajů daných tabulkou v zadání od hodnoty = 2 l s^-1. Tuto získáme nelineární regresí pro nezávislou proměnnou a závislou proměnnou (např. pomocí MAPLE).

Zdrojový text