Extrakce s nemísitelnými rozpouštědly - protiproud

Zadání

  10 kg směsi o složení 13 hm.% acetonu a 87 hm.% vody se celkem extrahuje 55 kg extrakčního činidla o složení 99 hm.% toluenu a 1 hm.% acetonu. Požadované složení acetonu v rafinátu je minimálně 2 hm.%. Kolik je třeba rovnovážných stupňů při protiproudém uspořádání? Extrakce probíhá při 20 °C.

Řešení

Schéma protiproudé extrakce:

Rovnice potřebné pro řešení (pro stupeň j): bilance mCWA,j-1 + mB UA,j+1 = mC WAj + mB UAj   rovnováha UAj = f (WAj)

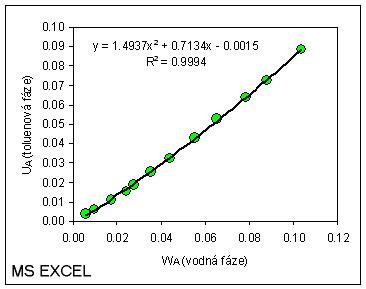
Rovnováha voda-aceton-toluen

Z e-tabulek získáme data pro rovnovážné složení mezi rafinátem a extraktem. Jedná se o hodnoty hmotnostního zlomku acetonu ve vodné a toluenové fázi. Ke každé fázi správně přiřadíme označení hmotnostních zlomků w (rafinát) a u (extrakt). V MS Excel (nebo v jiném programu, který umožňuje počítat regrese) vypočteme rovnici rovnováhy.

Vodná fáze (W) 0,0059 0,0096 0,0175 0,0240 0,0277 0,0354 0,0438 0,0553 0,0652 0,0782 0,0883 0,1038

Toluenová fáze (U) 0,0036 0,0059 0,0112 0,0154 0,0188 0,0251 0,0325 0,0426 0,0530 0,0636 0,0727 0,0883

Získaná rovnice rovnováhy:      UAj = - 0,0015 + 0,7134 WAj+ 1,4937 (WAj)2

Zadáno:

Přepočty

m_C = m_R0 w_CR0) = 10*0,87 = 8,7 kg
m_B = m_Sju_BS = 55*0,99 = 54,45 kg
W_AR0 = w_AR0/(1 - w_AR0) = 0,13/(1 - 0,13) = 0,149
U_ASj = u_ASj/(1 - u_ASj) = 0,01/(1 - 0,01) = 0,01
W_ARN = w_ARN/(1 - w_ARN) = 0,02/(1 - 0,02) = 0,02

Pro řešení nejprve zvolíme počet stupňů, poté musíme vytvořit soustavu rovnic 2 x N rovnic a tuto soustavu řešit. Pokud je výsledná hodnota W_ARn menší nebo rovná 0,02, nalezli jsme vhodný počet stupňů, jinak volbu počtu stupňů a řešení celé soustavy rovnic zopakujeme. 

Výsledek: Jsou třeba 2 stupně.

Zdrojový text řešení: enp.mws