Extrakce s omezeně mísitelnými rozpouštědly

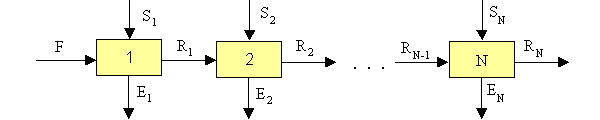
Opakovaná extrakce

Zadání
Do každého stupně extraktoru přivádíme 7 kg diethyletheru. Extrahujeme 30 kg směsi obsahující 75 hmotn. % vody a 25 hmotn. % kyseliny octové a požadujeme, aby koncentrace kyseliny octové v rafinátu z posledního stupně byla nejvýše 11,5 hmotn. %. Zjistěte potřebný počet stupňů, je-li v každém stupni dosaženo rovnováhy, a spotřebu extrakčního činidla. Extrakce probíhá při 25 stC.

Řešení

Rovnice potřebné pro řešení (pro stupeň j):

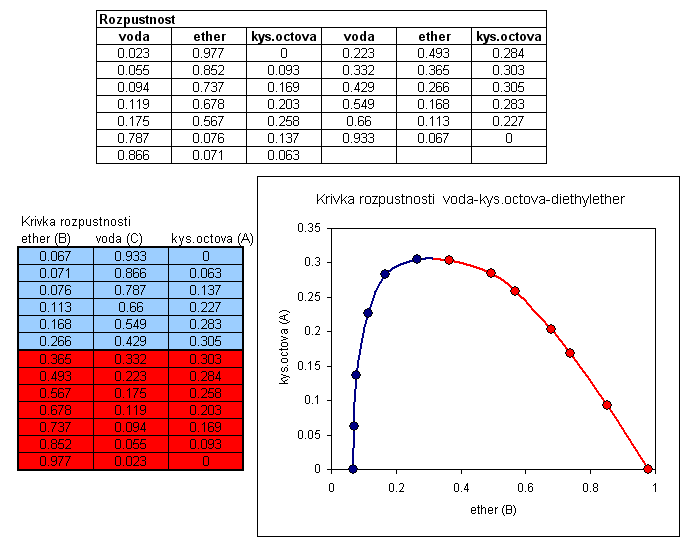
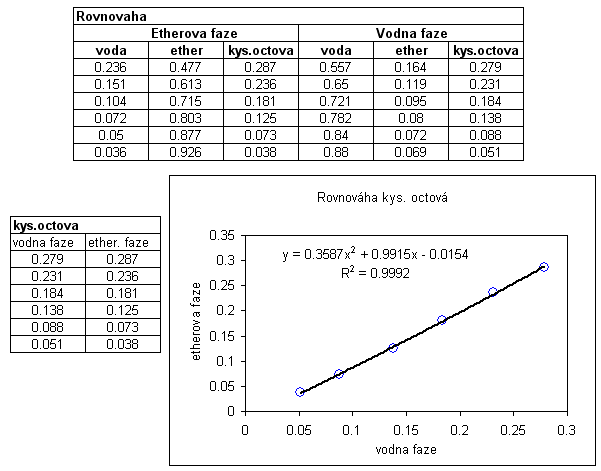
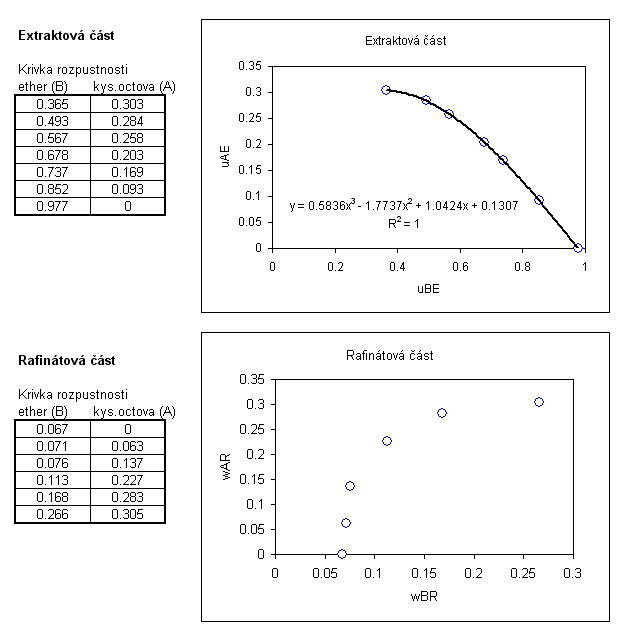
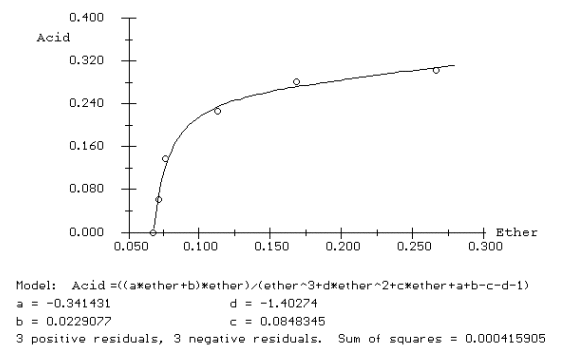
Rovnováha voda-kys.octová-diethylether a křivka rozpustnosti

Z e-tabulek získáme data pro rovnovážné složení kyseliny octové mezi vodnou a etherovou fází a z křivky rozpustnosti data pro binodálu rafinátové a extraktové části.  V MS Excel (nebo v jiném programu, který umožňuje počítat regrese) vypočteme rovnici rovnováhy a binodálu extraktové části. Pro popis rafinátové části binodály není možné užít polynomiální funkci, ale užíváme racionální lomenou funkci (viz. popis rovnováhy pro rektifikaci), jejíž parametry určíme nelineární regresí, např. v programu Polymath (Excel nelineární regresi neumí). Ukázky výpočtu:

Výpočet parametrů pro racionální lomenou funkci

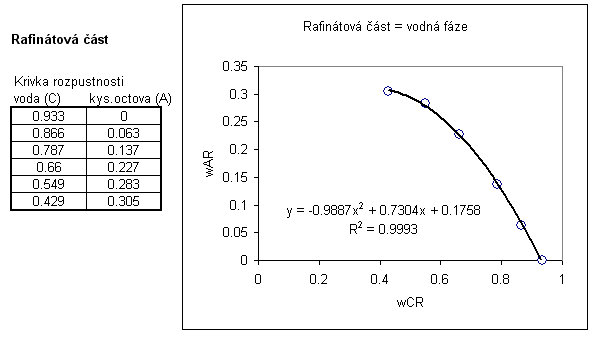
Druhou možností je vypočítat rafinátovou část binodály přes složky A (kys. octová) a C (voda). 
Místo funkce w_AR,j = f(w_BR,j) tak počítáme w_AR,j = f(w_CR,j). K popisu stačí polynomiální regrese:

Zadáno:

Opakovaně řešíme  soustavu 8 rovnic, dokud výsledné složení rafinátu je rovno, nebo menší než složení zadané.

Výsledek: S užitím racionální lomené funkce vyjde počet stupňů 3, s polynomem počet stupňů 4. Při manuálním (grafickém) řešení vyjdou také 4 stupně.

Zdrojový text řešení: eoo.mws