Výpočet průměru potrubí

Zadání
Z horského jezera, jehož hladina leží 100 m nad úrovní hydroelektrárny, se má vést nové ocelové potrubí dlouhé 1900 m, tak aby přetlak u ústí v elektrárně byl alespoň 0.588 MPa a množství proudící vody bylo 4 m³/min. Jaký má být průměr potrubí, jsou-li v potrubí zabudována 2 kolena 90°, uzavírací ventil, zpětná klapka a sací koš. Předpokládá se minimální teplota vody 10°C.

z₁ = 100 m
z₂ = 0 m
l = 1900 m
p₁ = p_atm
p₂ = p_atm + 58800 Pa
= 4 m³/min = 4/60 m³/s
l_e = 0,1 l
t = 10°C
p_atm = 101325 Pa

Řešení 

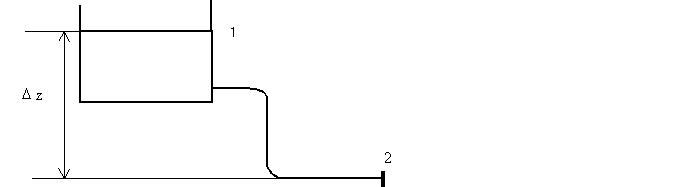
Pro potrubí, v němž není zařazeno čerpadlo, platí Bernoulliho rovnice mezi průřezy 1 a 2 zapsaná ve tvaru
 

p1 / r+ / 2 + z1 g = p2 / r +  / 2 + z2 g + edis1,2

(A)

Kapalina se čerpá ve směru od průřezu 1 k průřezu 2, p₁ je tlak nad hladinou nádrže, p₂ je tlak na konci potrubí, u₁ je rychlost hladiny, tedy rovna 0, střední rychlost v potrubí u₂ = u = / S (je objemový tok), g tíhové zrychlení a r hustota kapaliny. 

Člen e_dis1,2 je měrná ztrátová energie mezi průřezy 1 a 2, kterou vypočítáme ze vztahu 
 

(B)

kde l je součinitel tření , l délka potrubí a d jeho průměr. 

Výpočet součinitele tření l závisí na hodnotě Reynoldsova kritéria Re , které je pro trubku kruhového průřezu definováno vztahem
 

Re = u d r / h

(C)

kde rje hustota vody a hjejí dynamická viskozita, jejichž hodnoty pro danou teplotu nalezneme v tabulkách.

Až do hodnoty Re = 2300 závisí l jen na hodnotě Re. Oblast proudění, při níž Re < 2300 (pro tok uvnitř trubky), se nazývá laminární. Pro hodnoty Re>2300 závisí součinitel tření na hodnotě Re a absolutní drsnosti potrubí e vztahem

(D)

Hodnotu absolutní drsnosti e nalezneme v tabulkách pro materiál, z kterého je dané potrubí vyrobeno.

Předpokládáme , že Re > 2300 a řešíme současně rovnice A – D pro neznámý průměr d . Po dokončení výpočtu tento předpoklad ověříme.
 
 

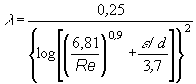Zdrojový text