Výpočet neznámé rychlosti v potrubí
[ZPĚT na OBSAH]
Zadání
  Chemický závod odebírá užitkovou vodu z horské nádrže, jejíž hladina je 150 m nad úrovní závodu. Potrubí má průměr 30 cm, je litinové, značně korodované, včetně ekvivalentních délek, zahrnujících místní odpory, je 3,2 km dlouhé. Přetlak na vstupu potrubí do závodu nemá klesnout pod 0,686 MPa. Předpokládá se minimální teplota vody 8°C. Jaký bude objemový tok vody, pokud nebude použito čerpadla.


p1 = patm
h1 – h2 = 150 m 
l + S l e = 3,2 km
d = 30 cm
p2 = patm + 0,686 MPa
t = 8°C

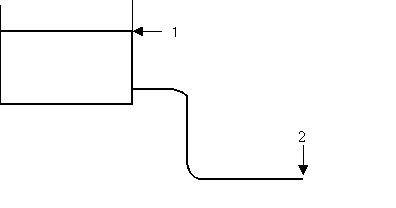
Řešení

Pro potrubí, v němž není zařazeno čerpadlo, platí Bernoulliho rovnice mezi průřezy 1 a 2 zapsaná ve tvaru

p1 / r+ / 2 + h1 g = p2 / r +  / 2 + h2g + edis1,2 (A) 

Kapalina se čerpá ve směru od průřezu 1 k průřezu 2, p1 je tlak nad hladinou nádrže, p2 je tlak na konci potrubí, u1 je rychlost hladiny (rovná 0), střední rychlost v potrubí u2 =u = / S (je objemový tok), g tíhové zrychlení a r  hustota kapaliny. 

Člen edis1,2 je měrná ztrátová energie mezi průřezy 1 a 2 kterou vypočítáme ze vztahu 
 
(B)
kde l je součinitel tření , l délka potrubí a d jeho průměr. 

Výpočet součinitele tření lzávisí na hodnotě Reynoldsova kritéria Re , které je pro trubku kruhového průřezu definováno vztahem
 
Re = u d r / h  (C)

kde r je hustota vody a h  její dynamická viskozita, jejichž hodnotu pro danou teplotu nalezneme v tabulkách.

Až do hodnoty Re = 2300 závisí l jen na hodnotě Re. Oblast proudění, při níž Re <2300 (pro tok uvnitř trubky), se nazývá laminární. Pro hodnoty Re > 2300 závisí součinitel tření na hodnotě Re a absolutní drsnosti potrubí e vztahem

(D)

Hodnotu absolutní drsnosti e nalezneme v tabulkách pro materiál, z kterého je dané potrubí vyrobeno.

Předpokládáme , že Re> 2300 a řešíme současně rovnice A – D pro neznámý objemový tok 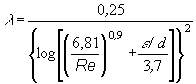. Po dokončení výpočtu tento předpoklad ověříme.
 

Zdrojovy textZdrojový text