Zadání Určete kolik se za den vyrobí tun (tj. produkce) ethylacetátu v ideálně míchaném průtočném reaktoru o objemu 7 m3. Ethylacetát se získává esterifikací kyseliny octové ethanolem. Počáteční koncentrace kyseliny octové je 4,2 kmol m-3, ethanolu 11 kmol m-3 a 16,5 kmol m-3 vody. Reakční rychlost může být popsána vztahem r = k1 cA cB – k2 cC cD . Za podmínek v reaktoru jsou hodnoty rychlostních konstant k1 = 8.10-9 m3 mol-1 s-1 a k2 = 2,55.10-9 m3 mol-1 s-1. Reakce bude zastavena, jakmile konverze kyseliny octové dosáhne hodnoty 0,3. Zjistěte také, jaká je možná maximální konverze kyseliny octové pro tento systém. Stechiometrická rovnice má tvar: CH3COOH + C2H5OH = CH3COOC2H5 + H2O Složky: A – kyselina octová, B – ethanol, C – ethylacetát, D – voda c A0 = 4,2 kmol m-3
k1 = 8.10-9 m3 mol-1 s-1 k2 = 2,55.10-9 m3 mol-1 s-1 z Ak = 0,3 t Z = 30 min V = 7 m3 r = k1 cA cB – k2 cC cD n A = -1
Řešení Pro výpočet produkce ethylacetátu (C) D chceme znát
Dosadíme a získáme vztah pro výpočet produkce
Jak je vidět musíme znát objemový tok reakční
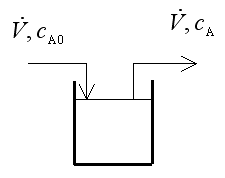
směsi vstup + zdroj = výstup
kde cA0, cA jsou molární koncentrace složky A na vstupu, resp. na výstupu, nA je stechiometrický koeficient složky A (je záporný, protože složka A zaniká) a r je reakční rychlost dané reakce. Protože se v rovnici pro reakční rychlost vyskytují molární koncentrace všech složek, musíme je před řešením vyjádřit v závislosti na konverzi složky A cA = cA0 (1-zAk ) , cB = cB0 - cA0zAk , cC = cA0zAk , cD = cD0 + cA0zAk . Maximální konverze je dosaženo, jestliže se systém dostane do rovnováhy, tj. že celková reakční rychlost složky A (nA r)je rovna nule. Vyjádříme si molární koncentrace v závislosti na maximální konverzi složky A. Koncentrace označíme indexem max, abychom je odlišily od těch, které již máme vyjádřené pomocí zadané konverze, stejně tak rychlosti reakce: cAmax = cA0 (1 - zAmax); cBmax = cB0 - zAmaxcA0; cCmax = cA0zAmax; cDmax = cD0 + zAmaxcA0; rAmax = k1 cAmax cBmax - k2 cCmax cDmax; Hledáme řešení, kdy nA r = 0 a víme, žezAmax nemůže být větší než 1. |
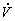 .
K jeho výpočtu použijeme látkovou bilanci
ideálně míchaného průtočného reaktoru pro složku A
.
K jeho výpočtu použijeme látkovou bilanci
ideálně míchaného průtočného reaktoru pro složku A