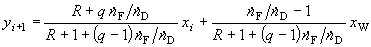Rektifikace

Zadání
Roztok ethanolu ve vodě obsahující 30% ethanolu má být zpracován na patrové rektifikační koloně tak, aby destilát obsahoval 80% ethanolu a zbytek 1%. (Všechna procenta jsou molární). Nástřik se přivádí při teplotě 20°C, kondenzátor je totální a vařák rovnovážný. V koloně je normální tlak a poměr zpětného toku má být roven dvojnásobku minimálního poměru zpětného toku. Kolik musí mít kolona teoretických stupňů, kolik teoretických a kolik skutečných pater, je-li celková účinnost kolony 0,6? Do kolikátého patra (počítáno odshora) je třeba přivádět nástřik? 

Zadaná data:
x_F = 0,3; x_D = 0,8; x_W = 0,01; R = 2 R_min; t_F = 20°C; E_c = 0,6 

Řešení
Pro výpočet počtu teoretických pater musíme znát hodnotu poměru zpětného toku R, který je zadán jako násobek minimální hodnoty. Tu spočteme tak, že nejprve určíme hodnotu veličiny q, která je dána vztahem 

q = (hVF - hF) / (hVF - hLF)

(A)

kde h_VF je molární enthalpie nasycené páry o složení nástřiku, h_LF molární enthalpie kapaliny o složení nástřiku při její teplotě varu a h_F molární enthalpie nástřiku. 

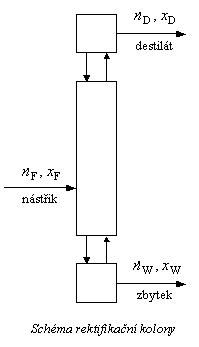
Pak řešíme rovnici

(q - 1) y = q x - xF

(B)

společně s rovnicí rovnováhy. Označíme-li výsledek řešení této soustavy x_m, y_m, platí

Rmin = (xD - ym)/(ym- xm)

(C)

Pro výpočet počtu teoretických stupňů napíšeme látkovou bilanci obohacovací části kolony mezi i-tým patrem a destilátem ve tvaru   yi+1 = R/(R + 1) xi + xD/(R +1)  (D) kde yi+1 je molární zlomek těkavější složky v páře vycházející z i+1 patra a xi je molární zlomek téže složky v kapalině vytékající z i-tého patra.  Pro ochuzovací části kolony (pod nástřikem) platí látková bilance ve tvaru   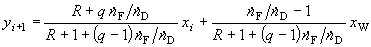(E)

Proudy které vycházejí z teoretického stupně musí být vzájemně v rovnováze. V dokumentu "Návod k popisu rovnováhy kapalina-pára" je v příkladu 3. ukázáno, že pro směs ethanol voda ve velkém rozsahu koncentrací vyhovuje rovnovážný vztah

yi = xi (a xi2 + b xi + c)/( xi3 + d xi2 + e xi + f )

(F)

kde a až f jsou empirické konstanty. Počet teoretických stupňú v obohacovací části kolony pak počítáme tak, že ze známé hodnoty y₁ = x_D vypočteme rešením rovnovážného vztahu (F) hodnotu x₁, tu dosadíme do rovnice (D) a tento postup opakujeme tak dlouho, dokud platí látková bilance obohacovací části kolony. Že je třeba přejít na bilanci ochuzovací části (E), poznáme tak, že vyřešíme soustavu rovnic (B) a (D). Označíme-li složení kapaliny, které z tohoto řešení vyjde x_p, končí obohacovací část kolony tam, kde naposledy platí x_i > x_p. Pak pokračujeme ve výpočtu stejně jako předtím, jen místo rovnice (D) používáme rovnici (E). V rovnici (E) se vyskytují poměry molárních toků proudů, pokud není žádný tok zadán, nejednodušeji je vypočteme tak, že zvolíme například molární tok nástřiku  100 kmol h^-1 a toky ostatních proudů vypočteme z celkové bilance a bilance těkavější složky (viz schéma) 

=  +

(G)

xF = xD + xW

(H)

Konec kolony je tam, kde x_i = x_W, hodnotu i pro kterou tato rovnost platí označíme N a je rovná potřebnému počtu teoretických stupňů. Rovnosti se většinou nepodaří pro celý počet teoretických stupňů dosáhnout, proto vypočteme poslední hodnotu x_i pro kterou ještě x_i > x_W a navíc vypočteme ještě x_i+1. 

Označíme-li tuto poslední hodnotu indexu i symbolem n, vypočteme potřebný počet teoretických stupňů lineární interpolací z rovnice

N = n +( xn - xW) / (xn - xn+1)

(I)

Rovnovážný vařák představuje 1 teoretický stupeň, počet theoretických pater N_th tedy je

Nth = N - 1

(J)

Počet skutečných pater N_sk vypočteme z počtu teoretických pater podle vztahu

Nsk = Nth/Ec

(K)

Zdrojový text