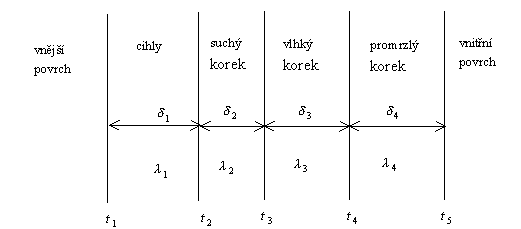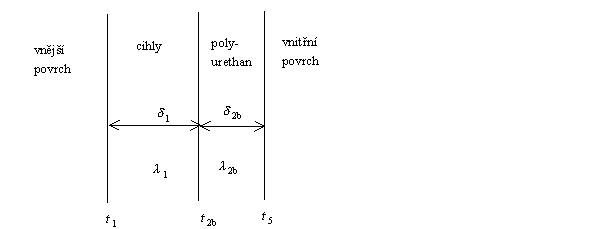Vedení tepla

Zadání

Rovinná stěna chladírny se skládá z vnější vrstvy stavebních cihel o tloušťce 0,30 m a vrstvy lisovaných korkových desek o celkové tloušťce 200 mm. Z vnějšku proniká do korku vzduch o rosném bodu 10 °C. Voda z něj vyloučená u vnitřního povrchu chladírny mrzne. Pro případ kdy teplota vnějšího povrchu cihlové stěny je 25 °C, teplota v chladírně -2 °C a za předpokladu, že tepelná vodivost vlhkého korku je dvakrát a promrzlého pětkrát větší než suchého vypočtěte intenzitu toku tepla stěnou chladírny a tloušťku vrstev suchého, vlhkého a promrzlého korku. Nevhodná stará korková izolace má být nahrazena polyurethanovou pěnou, která neprovlhá. Spočtěte potřebnou tloušťku polyurethanové vrstvy, má-li se při výměně izolace snížit intenzita toku tepla na polovinu původní hodnoty.

Řešení

a)Výpočet tloušťky vrstev suchého, vlhkého a promrzlého korku

Nejprve si nakreslíme schematický náčrt stěny chladírny

Význam symbolů je dostatečně patrný z obrázku.Vrstva suchého korku musí končit v místě, kde teplota izolace je rovná teplotě rosného bodu, vrstva promrzlého korku začíná tam, kde teplota klesne na 0 °C. Z této úvahy a z textu zadání plyne, že t₁ =25°C, t₃ = 10°C, t₄ =0°C, t₅ = -2°C, a teplotu t₂ neznáme. Je zadána tloušťka cihlové stěny d₁ =0,3 m a celková tloušťka korkové izolace 0,2 m, platí tedy
 

d2  + d3  + d4  = 0,2

(A)

Tepelnou vodivost stavebních cihel l₁ a suché korkové desky l₂ najdeme v Chemicko-inženýrských tabulkách (Tab.VI-1a), je l₁ = 0,6 Wm^-1K^-1 ; l₂ = 0,05 Wm^-1K^-1 . Ze zadání víme, že l₃ = 2l₂
a l₄ = 5l₂

Máme spočítat intenzitu toku tepla složenou stěnou chladírny q a tloušťky d₂ , d₃ a d₄. Potřebujeme tedy minimálně čtyři rovnice napsané tak, aby neobsahovaly neznámou teplotu t₂, nebo pět rovnic, pokud nechceme nad zápisem soustavy rovnic příliš přemýšlet. Při práci na počítači zvolíme druhý postup, protože je přehlednější a úspora jedné rovnice je nevýznamná. (Zkusíte-li si sestavit soustavu čtyř rovnic samostatně, možná Vám to neuškodí.) Protože v ustáleném stavu musí být intenzita toku tepla všemi vrstvami stejná, platí
 
 

q = (t1 - t2)l1 /d1	(B)
q = (t2 - t3)l2 /d2	(C)
q = (t3 - t4)l3 /d 3	(D)
q = (t4 - t5)l4 /d4	(E)

Soustavu rovnic (A) až (E) vyřešíme v MAPLE, procedura pro numerické řešení rovnic fsolve, která je standardní součástí MAPLE tuto soustavu nevyřeší, je třeba použít externí proceduru Newton, která vyžaduje zadání odhadů neznámých. Protože celá tloušťka korkové vrstvy je 0,5 m, a je rozdělena na tři vrstvy, zadáme pro všechny neznámé tloušťky odhad 0,07 m, teplota t₂ musí být mezi t₁ a t₃ , zadáme odhad 15°C a q odhadneme postupem uvedeným v programu.

a)Výpočet tloušťky nové izolace 

Nakreslíme si opět schematický náčrt stěny chladírny

Veličiny, které se proti původnímu uspořádání nezměnily jsou označeny stejnými symboly. Máme spočítat tloušťku nové polyurethanové izolace d_2b , víme-li, že pro novou intenzita toku tepla q_bmá platit

q_b = 0,5q

Pro tepelnou vodivost polyurethanové pěny najdeme v tabulkách l_2b = 0,03 Wm^-1K^-1 .

Z požadavku ustáleného stavu plynou rovnice
 
 

qb = (t1 - t2b)l1 /d1	(F)
qb = (t2b - t5)l2b /d2b	(G)

Vyřešíme je v MAPLE.

Výsledek.

Intenzita toku tepla stěnou chladírny byla 10 W m^-2, tloušťka vrstvy suchého, vlhkého a promrzlého korku byla 0,05; 0,1 a 0,05 m resp. Tloušťka nové izolace pro poloviční intenzitu toku tepla vychází 0,147 m, 
volíme 0,15 m.

Zdrojový text