1.1.2 Kompresor
Kompresor stlačuje vzduch o atmosférickém tlaku 100 kPa a teplotě 300 K na
tlak 400 kPa. Jaký příkon musí mít motor, aby kompresor stlačil 40
dm3 vzduchu za sekundu (měřeno za tlaku 100 kPa a teploty 300 K)?
Předpokládejte ideální chování a vratný průběh stlačování; jakékoliv ztráty
zanedbejte. Izobarická molární tepelná kapacita vzduchu je 29
J K−1 mol−1.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
2345 W
Postup
Použijeme Poissonovy rovnice pro vratný adibatický děj. Práci (za jednotku času) vypočteme z 1. věty a vztahu ΔU = CVΔT. Nakonec odečteme práci vykonanou atmosférou.
Audio
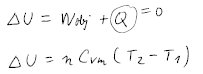
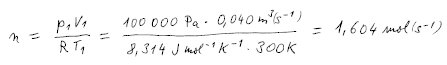
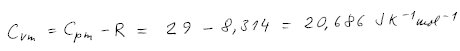
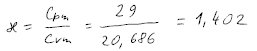
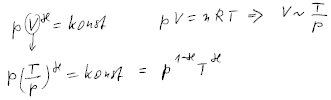
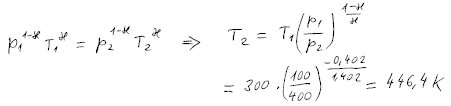
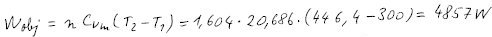
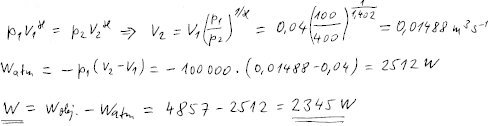
Kompresor stlačuje vzduch rychle, a proto lze předpokládat, že se jedná o
vratný adiabatický děj popsaný Poissonovými rovnicemi. Při výpočtu objemové
práce je nejlepší vyjít z první věty termodynamické. Protože teplo Q je
rovno nule, dostaneme, že objemová práce je rovna změně vnitřní energie. Tu
pro ideální plyn umíme spočítat ze změny teploty.
Nejprve spočítáme látkové množství plynu ze stavové rovnice ideálního plynu.
Protože počáteční objem máme zadán jako průtok, tj. objem za sekundu,
dostaneme vlastně látkové množství v molech za sekundu.
Izochorickou tepelnou kapacitu dostaneme z izobarické odečtením plynové
konstanty.
Poissonova konstanta je rovna poměru tepelných kapacit.
Poissonovu rovnici potřebujeme v proměnných tlak a teplota. Pokud si ji
nepamatujete, snadno ji odvodíte z rovnice v proměnných tlak a objem. Objem
je totiž úměrný poměru teploty a tlaku.
Nyní již můžeme spočítat konečnou teplotu.
A tak máme pohromadě vše pro výpočet objemové práce. Jedná se o práci za
sekundu, tedy výkon. Jednotka je Joule za sekundu neboli Watt.
Nakonec nesmíme zapomenout, že při stlačování nám pomáhá atmosféra. Odečteme
proto práci vykonanou atmosférou, opět za jednu sekundu. Počáteční i konečný
objem vypočteme z Poissonovy rovnice.