1.2.1 Stavová rovnice ideálního plynu
Uvažujme určité množství ideálního plynu při výchozí teplotě 20 °C a tlaku 100 kPa. Vypočtěte:
a) Při jakém tlaku bude plyn za dané teploty vykazovat poloviční objem?
b) Na jakou teplotu by bylo nutno ochladit původně přítomné množství plynu
(za konstantního tlaku), aby se jeho objem zmenšil na 75% původní hodnoty.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
(a) p2 = 200 kPa, (b) T2 = 219,86 K
Postup
a) ze stavové rovnice ideálního plynu, kam dosadíme podmínky (T1 = T2
=konst, n = konst)
b) podobně s tím, že podmínky jsou T1 = T2 = konst, n = konst
Audio
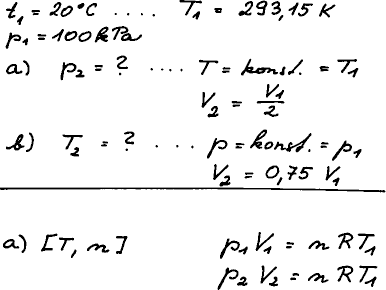
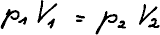
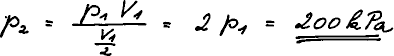
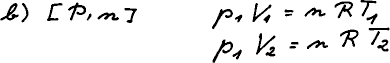
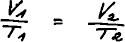
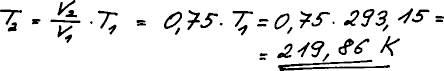
V průběhu příkladu se nemění látkové množství plynu n. V případě a) se
nemění ani teplota (izotermický děj). Zapíšeme si stavovou rovnici ideálního
plynu pro počáteční bod 1 a konečný bod 2. Teplota na konci T2 = teplota na
začátku T1.
Jestliže se rovnají pravé strany, rovnají se i levé. Kombinací
dostaneme rovnici zvanou Boyleův zákon. Platí pro ideální plyn za
konstantní teploty a jestliže se látkové množství plynu nemění.
Jedinou neznámou je konečný tlak p2.
V případě b) se jedná o izobarický děj. Zapíšeme stavovou rovnici pro
počáteční bod 1 a stejnou rovnici pro bod 2. Tlak na počátku p1 = tlak
na konci = p2.
Kombinací dostaneme vztah (Gay-Lusacův zákon), který platí pro ideální plyn za
konstantního tlaku a látkového množství.
Jedinou neznámou je konečná teplota T2.