1.4.1 Změna entropie při vratném adiabatickém ději
Určete změnu entropie při vratné adiabatické expanzi jednoho molu ideálního plynu ze stavu T1 = 300 K, p1 = 200 kPa na teplotu T2 = 250 K. Poissonova konstanta má hodnotu κ = 1,4.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
ΔSm = 0. Jedná se totiž o vratný adiabatický děj, tedy o děj izoentropický.
Postup
pro vratný děj, 
pro adiabatický děj, a proto
dS = a po integraci přes celý děj ΔS = 0.
Audio
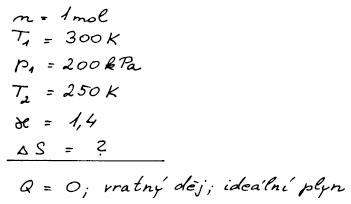
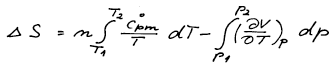
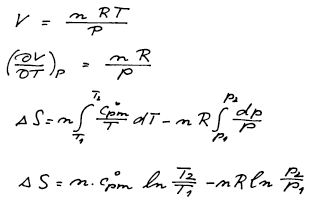
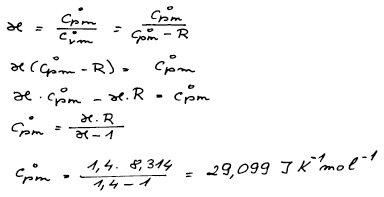
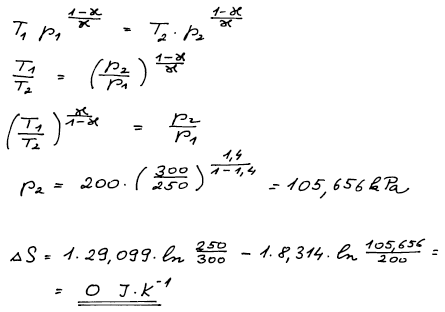
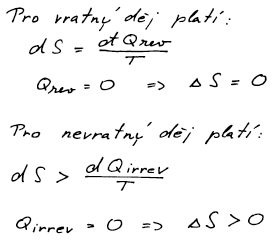
Děj adiabatický vratný, ideální plyn, tepelné kapacity jsou konstantní
V systému se mění teplota a tlak, změnu entropie vyjádříme jako funkci teploty a tlaku
Integrujeme za předpokladu, že systém tvoří ideální plyn a tepelné kapacity jsou konstantní.
Pro výpočet entropie je třeba nejprve vypočítat Cp,m° a
tlak p2. Molární tepelnou kapacitu Cp,m° vypočteme
z Poissonovy konstanty a konečný tlak z Poissonovy rovnice (platí pro
vratný adiabatický děj, objemová práce, ideální plyn, konstantní
tepelné kapacity)
Výsledek – změna entropie se rovná nule. Tím jsme potvrdili, že vratný adiabatický děj je děj izoentropický.
Z II. věty termodynamické plyne: a) vratný adiabatický děj = entropie je konstantní, b) nevratný adiabatický děj = entropie roste.