1.7.6 Výpočet pH
V 1 litru vody bylo rozpuštěno 0,1 g mravenčí kyseliny (M = 46 g mol−1). Vypočítejte pH roztoku. Disociační konstanta mravenčí kyseliny pro standardní stav nekonečného zředění (cst = 1 mol dm−3) má hodnotu 1,77 . 10−4. Předpokládejte, že aktivitní koeficienty látek vzhledem ke standardnímu stavu nekonečného zředění jsou jednotkové.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
pH = 3,27
Postup
Základem řešení je bilance disociace kyseliny mravenčí na ionty. Část kyseliny zůstane nedisociovaná. Do vztahu K = a(H+) . a(A−)/a(HA) dosadíme z bilance aktivity podle ai = ci/cst.
Audio
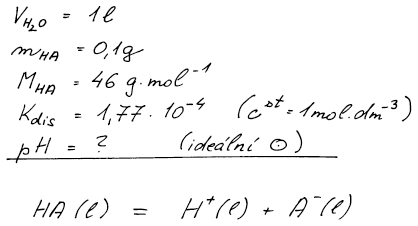
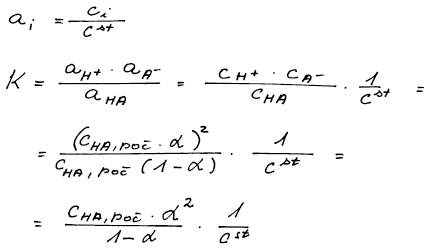
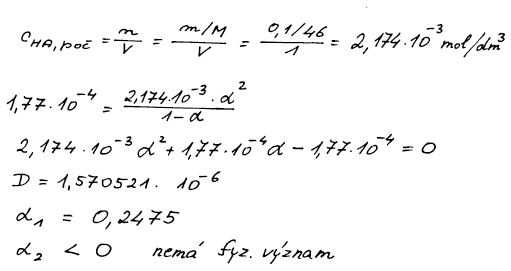
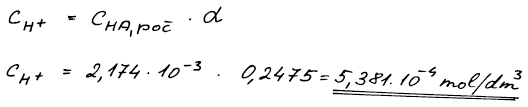
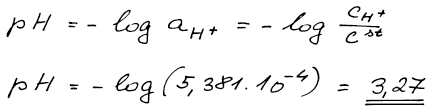
Kyselina mravenčí je ve vodě slabá kyselina, která se ve vodném
roztoku částečně disociuje. Na tuto disociaci se budeme dívat jako na
jakoukoli jinou chemickou reakci. Rovnovážná konstanta této reakce se
nazývá disociační konstanta.
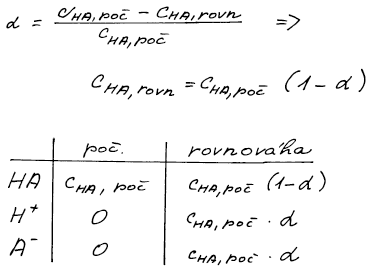
Řešení příkladu s chemickou rovnováhou začínáme vždy bilanční
tabulkou, kde budeme bilancovat molární koncentrace tj. počty molů
v jednotce objemu. K vyjádření koncentrace iontů i nerozdisociované
kyseliny využijeme stupeň přeměny α.
Ve vztahu pro rovnovážnou konstantu nahradíme aktivity kapalných
složek měřitelnými veličinami – molárními koncentracemi v rovnováze.
Pro rozpuštěnou látku volíme standardní stav nekonečného zředění (cst = 1 mol dm−3). Dále je uvažován ideální roztok.
Koncentraci kyseliny na počátku snadno spočteme ze zadaných
údajů. Rovnice pro rovnovážnou konstantu pak už obsahuje pouze jednu
neznámou – stupeň přeměny α. Ten získáme řešením kvadratické rovnice.
Pro vypočet žádaného pH roztoku potřebujeme nejprve zjistit
koncentraci vodíkových iontů v rovnováze. Tu vypočteme pomocí výrazu
odvozeného v bilanční tabulce.
pH roztoku je definováno jako záporný dekadický logaritmus aktivity
vodíkových iontů. Aktivitu opět převedeme na molární koncentraci a pak
už jen dosadíme.