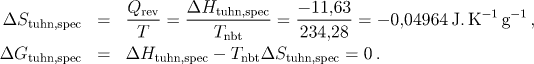10.2.1 Aplikace Clapeyronovy rovnice
Normální teplota tání rtuti je −38,87 °C. Za této teploty je
hustota její kapalné fáze 13,6537 g.cm−3 a tuhé fáze 14,2572 g cm−3.
Entalpie tání má hodnotu 11,63 J g−1.
Předpokládejte, že všechny udané hodnoty (mimo teplotu tání) jsou
nezávislé na tlaku a teplotě a vypočítejte:
a) teplotu tání rtuti za tlaku 20 MPa, b) hodnoty ΔS
a ΔG odpovídající ztuhnutí 1 g kapalné rtuti při
teplotě -38,87 °C a normálním tlaku.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
a) ΔVtuhn,spec = −3,1 . 10−6 m3. kg−1 a T2 = 235,48 K
b) ΔStuhn,spec = −0,04964 J K−1 g−1 a
ΔGtuhn,spec = 0.
Postup
V obou hustot vypočteme změnu specifického objemu a dosadíme do integrované Clapeyronovy rovnice (10.3)
Řešení
a) Poněvadž jde o fázový přechod 
(tuhnutí), musíme
pro výpočet vlivu tlaku na teplotu tání (nebo tuhnutí, u čistých
látek je to totéž) použít Clapeyronovu rovnici
Vzhledem k tomu, že se jedná o konečnou změnu tlaku, budeme vycházet z integrované rovnice a z předpokladu, že poměr ΔH/ΔV nezávisí na teplotě, resp. na tlaku. Po separaci proměnných a integraci v mezích dostaneme
kde ΔHtuhn,spec a ΔVtuhn,spec představují změnu entalpie a objemu při tuhnutí látky o jednotkové hmotnosti. Pro rtuť za uvedených podmínek platí:
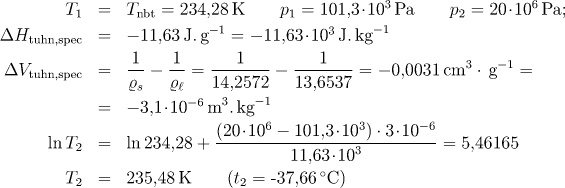
b) Z definiční rovnice entropie a Gibbsovy energie vyplývají vztahy
