4.1.19 Změna entropie při nerovnovážném izotermickém fázovém přechodu
Vypočítejte změnu entropie pro nerovnovážný izotermický fázový přechod, při kterém podchlazená voda o teplotě −10 °C přejde na led o stejné teplotě. Molární tepelná kapacita ledu je 37,68 J mol−1 K−1, ostatní potřebné hodnoty nalezněte v tabulkách. Posuďte, zda výsledek neodporuje II. větě termodynamiky.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
ΔSsyst = −20,56 J K−1
ΔHt(263,15) = 6040 J ΔSokolí = 24,31 J K−1
ΔScelk = 3,75 J K−1
Řešení
 V tabulkách nalezneme
entalpii tání ledu při 0 °C (6,01 kJ mol−1) a molární
tepelnou kapacitu vody (76,36 J K−1mol−1).
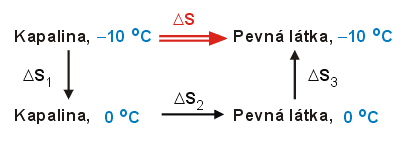
Děj je nerovnovážný, a tak je nutno najít náhradní sled vratných
dějů, při nichž by se kapalná voda dostala z daného počátečního do
daného konečného stavu. S ohledem na zadané veličiny je možno
zvolit postup, naznačený uvedeným schématem.
V tabulkách nalezneme
entalpii tání ledu při 0 °C (6,01 kJ mol−1) a molární
tepelnou kapacitu vody (76,36 J K−1mol−1).
Děj je nerovnovážný, a tak je nutno najít náhradní sled vratných
dějů, při nichž by se kapalná voda dostala z daného počátečního do
daného konečného stavu. S ohledem na zadané veličiny je možno
zvolit postup, naznačený uvedeným schématem.
Celková změna entropie je rovna součtu entropických změn pro jednotlivé dílčí pochody. Protože je molární teplo tuhnutí rovno molárnímu teplu tání s opačným znaménkem, platí vztah:
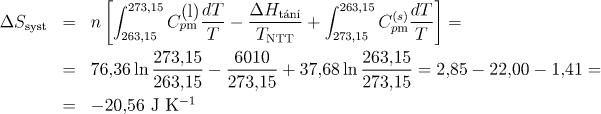
Uvažovaný děj je samovolný. Záporné znaménko však není překvapující (děj není adiabatický), uvědomíme-li si, že musíme uvažovat nejen změnu entropie systému (vody), ale i okolí, abychom mohli ze znaménka usuzovat na vratnost děje. Okolí by v daném případě mohl tvořit obrovský zásobník o t = −10 °C, který by byl trvale v kontaktu s daným systémem (podchlazenou vodou). Pro výpočet tepla, které systém během tuhnutí uvolní do okolí, pochod opět rozdělíme na tři dílčí vratné děje. Analogicky jako u výpočtu celkové změny entropie při tuhnutí vody dostaneme
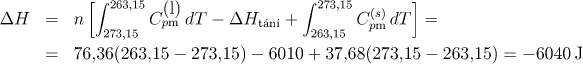
Zásobník tedy přijme teplo 6040 J. Protože je hmotnost zásobníku o mnoho řádů vyšší, než hmotnost systému, teplota zásobníku se přijetím uvedeného tepla prakticky nezmění. Platí tedy
![]()
Celková změna molární entropie
![]()
je kladná, což je v souladu se spontánním průběhem izotermického fázového přechodu.