4.3.1 Výpočet absolutní entropie ze III. věty termodynamiky
S použitím dále uvedených dat vypočítejte absolutní molární entropii
jednoklonné síry při teplotě 373,15 K a tlaku 101,325 kPa.
Síra existuje v kosočtverečné krystalické
modifikaci do teploty 368,46 K, potom přechází na síru
jednoklonnou. Teplo této fázové přeměny má hodnotu 0,4017
kJ/mol. Normální teplota tání jednoklonné síry je 388,36 K a
molární teplo tání má hodnotu 1,717 kJ/mol.
Hodnoty molárních tepelných kapacit ( J mol−1 K−1):
Kosočtverečná síra v intervalu 20 až 298,15 K:
| T/ K | 20 | 40 | 60 | 80 | 100 | 150 | 200 | 250 | 298,15 |
| Cpm | 2,57 | 6,08 | 8,72 | 10,9 | 12,8 | 16,62 | 19,41 | 21,31 | 22,60 |
Jednoklonná síra v intervalu 368,46 až 388,36 K:
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
ΔSm0 → 20 = 0,8567 J mol−1 K−1
ΔSm20 → 298,15 = 30,826 J mol−1 K−1
ΔSm298,15 → 368,46 = 5,018 J mol−1 K−1
ΔSmkos. → jedn. =1,090 J mol−1 K−1
ΔSm368,46 → 373,15 = 0,325 J mol−1 K−1
= 38,116 J mol−1 K−1
Řešení
Podle třetí věty termodynamiky je absolutní entropie
kosočtverečné síry při absolutní nule nulová. Absolutní
entropie síry je tedy
rovna součtu dílčích změn entropie při přechodu ze stavu
= 0 K; 101,325 kPa) do stavu
(
= 373,15 K; 101,325 kPa).
1. Ohřev kosočtverečné síry z absolutní nuly do teploty
modifikační přeměny.
Protože je v tomto teplotním rozsahu molární tepelná kapacita
zadána různými způsoby (Debyeův vztah, tabulka a polynom),
změnu entropie při tomto pochodu vyjádříme jako součet tří dílčích
hodnot: změny entropie v intervalu 0 až 20 K, změny entropie
v intervalu 20 až 298,15 K a změny entropie při ohřevu od 298,15 K do
bodu zvratu.
Pro interval 0 až 20 K využijeme Debyeova vztahu (4.20)
Konstantu a vypočítáme porovnáním této rovnice s hodnotou molární tepelné kapacity při teplotě 20 K (první hodnota v tabulce v zadání):
Pro změnu entropie získáme hodnotu
Hodnotu změny entropie při ohřevu z teploty 20 K na teplotu 298,15 K vypočítáme z tabelovaných hodnot molární tepelné kapacity numerickou integrací pomocí lichoběžníkového pravidla. Hodnota změny entropie je dána vztahem
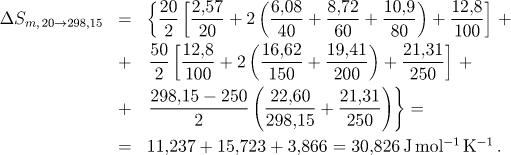
Změnu entropie při ohřevu z 298,15 K na teplotu modifikační přeměny vypočítáme analytickou integrací
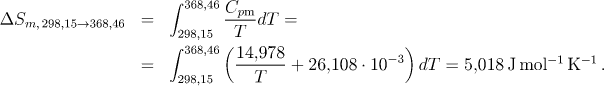
2. Přeměna kosočtverečné síry na jednoklonnou. Jde o izotermicko-izobarickou fázovou přeměnu. Pro změnu entropie proto platí (molární teplo modifikační přeměny dosazujeme v J/mol):
3. Ohřev jednoklonné síry na konečnou teplotu. Změnu entropie vypočítáme analogicky jako u síry kosočtverečné:
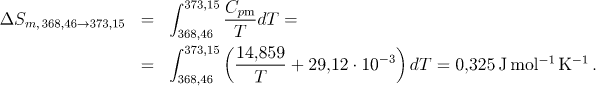
Celková změna entropie, která je dána součtem všech dílčích změn, zároveň představuje hodnotu absolutní entropie síry při daných podmínkách
Analogickým způsobem by bylo možno pokračovat, až bychom získali absolutní entropii ve stavu ideálního plynu.