5.1.2 Entalpie, entropie a Gibbsova energie ideální plynné směsi
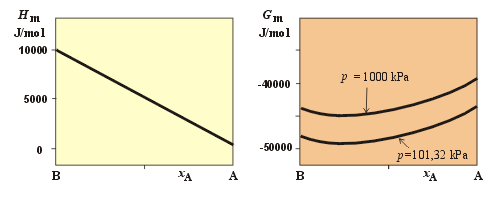
U plynné směsi, která obsahuje 30 mol.% látky A a 70 mol.% látky B vypočtěte molární entalpii, entropii a Gibbsovu energii při teplotě 298,15 K a tlaku 1000 kPa. Předpokládejte platnost stavové rovnice ideálního plynu jak pro čisté látky, tak i pro směs. Načrtněte Hm a Gm při konstantní teplotě v závislosti na x1 za standardního tlaku a za tlaku 1000 kPa. Při výpočtu použijte následujících dat (p° = 100 kPa):
| Látka | H°m(298,15 K, p°)/(J/mol) | S°m(298,15 K, p°)/( J mol−1 K−1) |
| A(1) | 1000 | 150 |
| B(2) | 10000 | 200 |
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
Hm(T, p, x) = 7300 J/mol, Sm(T, p, x) = 170,935 J mol−1 K−1, Gm(T, p, x ) = −43664 J/mol.
Řešení
Pro molární entalpii ideální směsi ideálních plynů dostaneme podle vztahu (5.2)
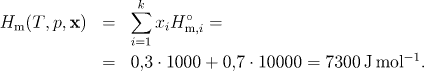
Entalpie ideálního plynu nezávisí na tlaku, a proto získaná hodnota platí pro jakýkoliv tlak.
Molární entropie směsi ideálních plynů je dána vztahem (5.3) a po dosazení zadaných údajů získáme entropii směsi
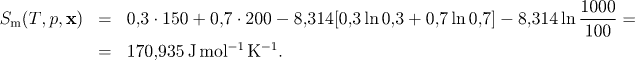
Molární Gibbsovu energii určíme z definičního vztahu, tj. ze vztahu (5.4)
![]()
Průběhy Hm a Gm jsou schematicky načrtnuty na následujícím obrázku.