Extrakce - nemísitelná rozpouštědla

UCHI VSCHT

Extrakce s omezeně mísitelnými rozpouštědly

Protiproudá extrakce

Zadání

30 hmotn. % kyseliny octové ve vodě se extrahuje při protiproudu čistým diethyletherem tak, aby koncentrace kyseliny octové ve vodě klesla na 3 hmotn. % a extrakt obsahoval 17 hmotn. % kyseliny octové. Určete potřebnou výšku vrstvy výplně a spotřebu ethyletheru na 1 kg suroviny. Extrakce probíhá při 25st C. Výška ekvivalentní rovnovážnému stupni je 0,75 m.

Řešení

Schéma protiproudé extrakce:

Označení složek
A - extrahovaná složka (kys.octová)
B - přidávané rozpouštědlo (diethylether)
C - původní rozpouštědlo (voda)

Označení proudů
F (R₀) - surovina
S - extrakční činidlo
R - rafinát
E - extrakt

Označení hmotnostních zlomků
w - surovina, rafinát
u - extrakční činidlo, extrakt

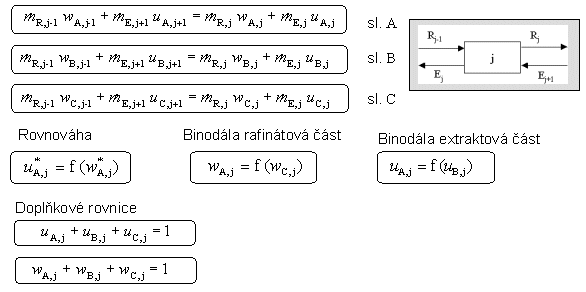
Rovnice potřebné pro řešení (pro stupeň j):

Rovnice potřebné pro rovnováhu a pro popis křivky rozpustnosti jsou popsané v předcházejícím příkladu. Užijeme rovnice vyjádřené polynomy.

Zadáno:

m_R0 = 1 kg
w_A0 = 0,30
w_B0 = 0
w_C0 = 0,70

u_AS = 0
u_BS = 1
u_CS = 0

Hledáme počet množství extrakčního činidla tak, aby w_AN = 0,03 a u_A1 = 0,17

Pro výpočet množství extrakčního činidla řešíme bilanci celého extraktoru.
Výsledek: Je potřeba 1,26 kg extrakčního činidla.

Zadáno:

m_R0 = 1 kg
w_A0 = 0,30
w_B0 = 0
w_C0 = 0,70

m_S = 1,26 kg
u_AS = 0
u_BS = 1
u_CS = 0

Hledáme počet stupňů (N), tak aby w_AN < 0,03

Pro řešení nejprve zvolíme počet stupňů, poté musíme vytvořit soustavu rovnic 8 x N rovnic a tuto soustavu řešit. Pokud je výsledná hodnota w_AN menší nebo rovná 0,03, nalezli jsme vhodný počet stupňů, jinak volbu počtu stupňů a řešení celé soustavy rovnic zopakujeme. Počet teoretických stupňů vynásobíme výškou ekvivalentní teoretickému patru.

Výsledek: Výška kolony je 2,98 m.

Zdrojový text řešení: eop.mws