1.3.9 Hessův zákon
Z údajů o rovnicích (1) a (2) při T= 298,15 K stanovte
a) ΔrH°3, ΔrU°3 pro reakci (3)
b) ΔslučH°(HCl,g)
při teplotě 298,15 K. Předpokládejte ideální chování plynů.
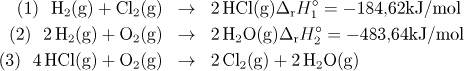
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
a) ΔrH°3 = −114,40 kJ mol−1, ΔrU°3 = −111,92 kJ mol−1; b) ΔslučH°(HCl,g) = −92,31 kJ mol−1
Postup
Reakci (3) (a proto i její entalpii) vyjádříme jako lineární kombinaci rovnic (1) a (2). Převedeme na vnitřní energii odečtením ΔrnRT. Slučovací rovnice HCl je polovinou reakce (1).
Audio
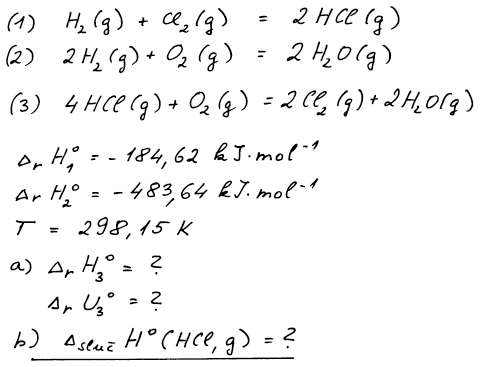
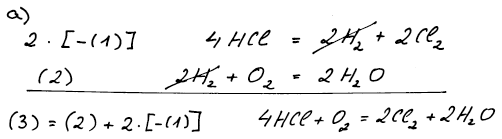
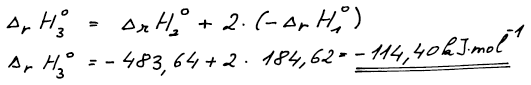
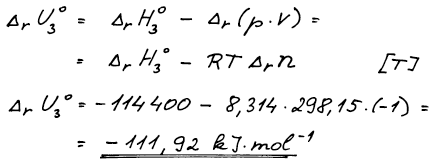
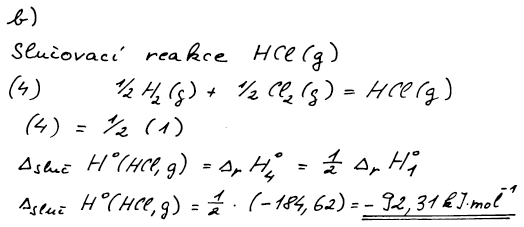
K řešení využijeme Hessův zákon, tj. budeme se snažit lineární
kombinací rovnic (1) a (2) získat požadovanou reakci (3).
Rovnice (3) vznikne, jestliže vezmeme rovnici (2) a od ní odečteme
dvojnásobek rovnice (1).
Při výpočtu reakční entalpie rovnice (3) na reakční entalpie reakcí
(1) a (2) aplikujeme stejnou lineární kombinaci jako v případě rovnic.
Změnu vnitřní energie reakce (3) vypočteme z definice
entalpie. Vzhledem k tomu, že všechny zúčastněné látky jsou plynné a
chovají se ideálně, je možno využít stavovou rovnici ideálního
plynu. Δrn reakce je rozdíl počtu molů plynných produktů
mínus počet molů plynných výchozích látek v rovnici (3), to je −1.
Slučovací entalpie HCl je reakční entalpie slučovací reakce
HCl. Zapíšeme si slučovací reakci, tj. reakci, při které vzniká 1 mol
látky z prvků. Při pohledu na rovnici (1) zjistíme, že rovnice (1) je
dvojnásobkem slučovací rovnice HCl. A tak slučovací entalpii vypočteme
jako polovinu reakční entalpie rovnice (1).