1.3 Základy termodynamiky I
Tato kapitola je věnována aplikaci první věty termodynamické
![]()
Symbol ΔU značí změnu vnitřní energie, Q teplo vyměňované s okolím a W práci; budeme uvažovat pouze objemovou práci.
Další stavová veličina, entalpie, je definována vztahem
![]()
Teplo, které soustava vymění s okolím za stálého tlaku a složení, je dáno změnou entalpie. Nedochází-li přitom k žádnému fázovému přechodu, platí pro změnu entalpie při změně teploty z T1 na T2
![]()
kde Cp = nCpm je tepelná kapacita za stálého tlaku (= izobarická) a Cpm molární tepelná kapacita za stálého tlaku.
Mayerův vztah mezi tepelnými kapacitami za konstantního tlaku a objemu
![]()
platí pro ideální plyn.
Střední tepelná kapacita je definována vztahem
![]()
Uvažujme reakci zapsanou formálně jako
![]()
kde pro stechiometrické koeficienty výchozích látek platí νi < 0 a produktů νi > 0. Reakční teplo u reakce probíhající za stálého tlaku je rovno změně entalpie a u reakce za stálého objemu změně vnitřní energie. Mezi oběma veličinami platí vztah
![]()
Hessův zákon říká, že je-li nějaká reakce lineární kombinací jiných reakcí, je stejnou lineární kombinací i její reakční entalpie. Po aplikaci na slučovací resp. spalné reakce dostaneme vzorce používané pro výpočet reakčních entalpií z tabelovaných hodnot slučovacích resp. spalných entalpií:
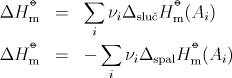
Kirchhoffova věta slouží k přepočtu reakční entalpie při jedné teplotě na jinou teplotu
![]()
kde
![]()
Příklady:
1.3.1 Výpočet tepla, práce, změny vnitřní energie a entalpie při izochorickém ději (1.3.2 Výpočet tepla a práce při izobarickém ději (
1.3.3 Výpočet práce při izotermním vratném ději (
1.3.4 Adiabatická vratná komprese (
1.3.5 Vratná neadiabatická expanze (
1.3.6 Změna entalpie (
1.3.7 Hessův zákon (
1.3.8 Kirchhoffova věta (
1.3.9 Hessův zákon (