1.3.7 Hessův zákon
Na základě reakčních entalpií následujících reakcí při 25 °C
R1: C(s) + O2(g) = CO2(g) ΔH°1 = −393,7 kJ/mol
R2: S(s) + O2(g) = SO2(g) ΔH°2 = −297,3 kJ/mol
R3: CS2(l) + 3 O2(g) = CO2(g) + 2 SO2(g) ΔH°3 = −1109.5 kJ/mol
vypočítejte slučovací entalpii CS2(l) při 25 °C.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
121,2 kJ/mol
Postup
Buď vyjádříme slučovací entalpii CS2 z R3, použivše slučovací entalpie ostatních látek z R1 a R2, nebo zkombinujeme reakce tak, abychom dostali slučovací reakci CS2.
Audio
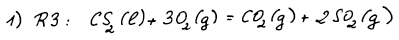
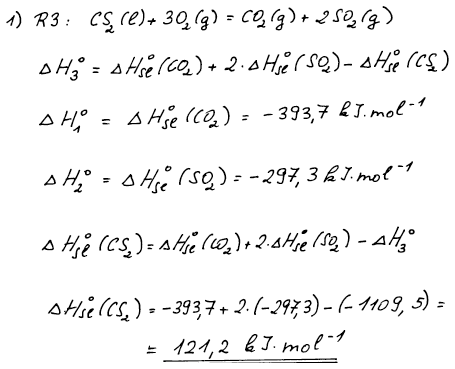
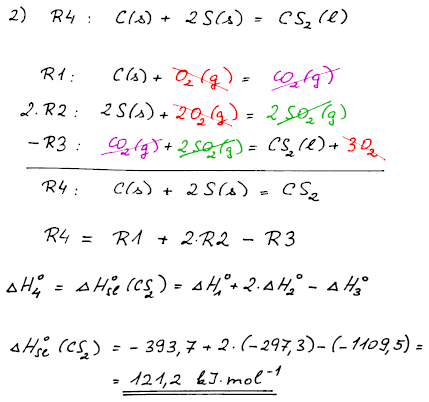
Můžeme postupovat dvěma způsoby. V prvním vypočteme slučovací
entalpii sirouhlíku z rovnice 3. K tomu potřebujeme znát slučovací
entalpie všech ostatních látek účastnících se této reakce. V druhém
případě vyjdeme z definice slučovací reakce a rovnice ze zadání
kombinujeme tak, abychom jejich kombinací získali požadovanou
slučovací rovnici.
Na rovnici R3, kde vystupuje sirouhlík, aplikujeme Hessův zákon –
entalpie reakce se vypočte jako rozdíl standardních slučovacích
entalpií produktů a výchozích látek násobených
příslušnými stechiometrickými koeficienty. Kyslík je prvek a slučovací
entalpie prvků je nulová. Reakce R1 je slučovací reakce CO2 a reakce
R2 je slučovací reakce SO2.
Vyjdeme ze slučovací reakce sirouhlíku = R4. Tuto reakci se pokusíme
získat lineární kombinací z rovnic, které máme k dispozici v zadání
příkladu. Stejnou kombinaci, kterou jsme uskutečnili s rovnicemi, pak
aplikujeme na reakční entalpie těchto reakcí a získáme reakční
entalpii slučovací reakce sirouhlíku tj. ΔHsl°(CS2)