1.3.5 Vratná neadiabatická expanze
Jeden mol dusíku, o němž předpokládáme, že se chová ideálně, expandoval vratně z tlaku 4,15 MPa a teploty 1000 K na teplotu T2 = 300 K. Při expanzi bylo s okolím vyměněno teplo Q = −2800 J. Uvažujeme-li, že Cpm° = 29,3 J K−1 mol−1, vypočítejte práci a změnu entalpie spojené s uvedeným dějem.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
W = −11 890 J, ΔH = 20 510 J
Postup
Expanze plynu není nijak specifikována, proto pro výpočet práce musíme využít 1. větu.
Audio

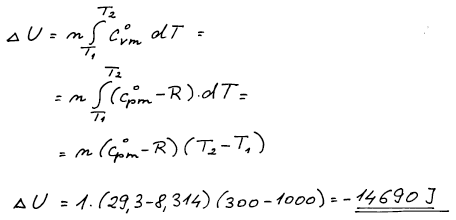
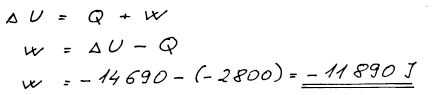
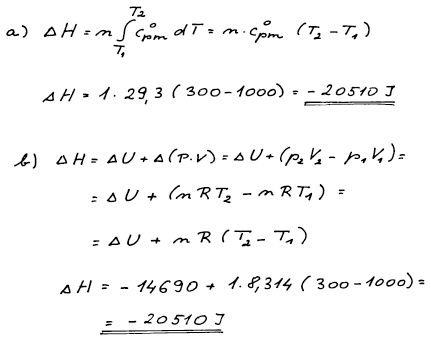
Expanze plynu není nijak specifikována, tj. není známa cesta, po které
systém dospěl z bodu jedna do bodu dva. A jelikož neznáme cestu
nemůžeme počítat práci přímo. Umíme ale vypočítat změnu vnitřní
energie, protože vnitřní energie je stavová veličina, která nezávisí
na cestě, ale jen na počátečním a konečném stavu.
Pro ideální plyn je vnitřní energie jen funkcí teploty.
Práci dopočteme z 1. věty termodynamické. Systém expanduje, tj. koná
objemovou práci a proto práce musí mít záporné znaménko.
Pro výpočet změny entalpie můžeme využít buď a) její teplotní
závislost nebo b) její definici.