1.4.7 Závislost entropie na p, V, T
Vypočtěte změnu entropie, která doprovází zahřátí jednoho molu H2S(g) z teploty 50 °C a počátečního tlaku 101,32 kPa na teplotu 100 °C za konstantního objemu a následující izotermní expanzi do stavu, kterému odpovídá tlak 101,32 kPa. U sulfanu (sirovodíku) předpokládejte, že se chová jako ideální plyn. Jeho izobarická molární tepelná kapacita je dána vzorcem Cpm/(J K−1 mol−1) = 30 + 13,8 . 10−3 T/K.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
ΔSm = 5,006 J K−1 mol−1
Postup
Sled obou dějů lze nahradit jedním izobarickým dějem a entropie je daná jedním integrálem za konst. tlaku.
Audio
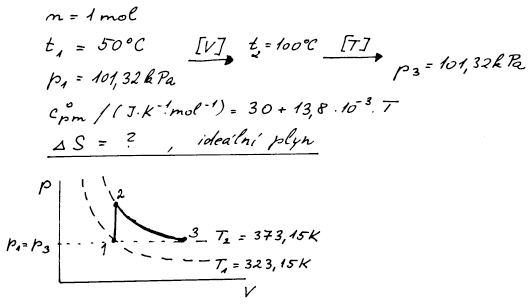
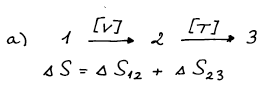
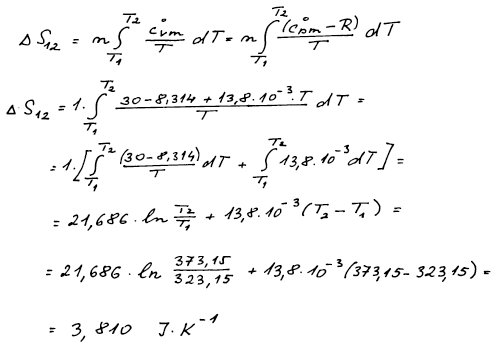
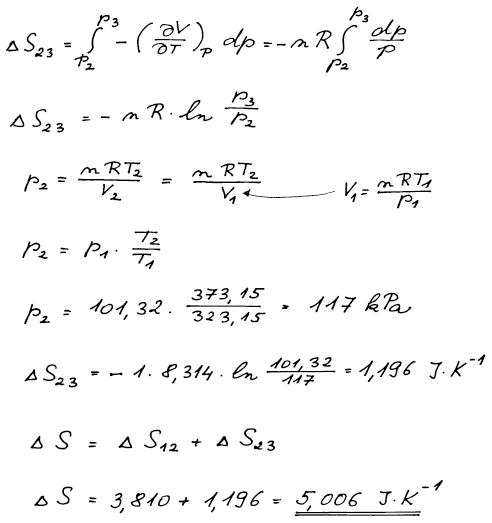
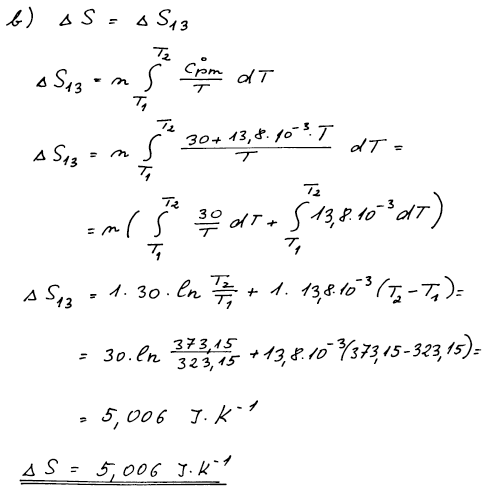
Entropie je stavová veličina – její změna nezávisí na cestě, ale jen
na počátečním a konečném stavu. Z obrázku je zřejmé, že umíme spočítat
změnu entropie po dvou cestách
a) cestu z bodu 1 přes bod 2 do bodu 3
b) přímou cestu po izobaře z bodu 1 do bodu 3
a) cestu z bodu 1 přes bod 2 do bodu 3
b) přímou cestu po izobaře z bodu 1 do bodu 3
Výpočet za a) si rozdělíme na izochorickou změnu entropie mezi body 1
a 2 a izotermní změnu entropie mezi body 2 a 3.
ΔS12 vypočteme z teplotní závislosti entropie za konstantního
objemu. Molární tepelnou kapacitu ideálního plynu za konstantního
objemu určíme pomocí Mayerova vztahu ze známé molární tepelné kapacity
za konstantního tlaku.
ΔS23 vypočteme ze závislosti entropie na tlaku za
konstantní teploty.
Výpočet za b) izobarického děje mezi body 1 a 3 – změnu entropie
vypočteme z teplotní závislosti entropie za konstantního tlaku.
Výsledná změna entropie musí být stejná, ať využijeme cestu za a) nebo
za b).