1.6.1 Clapeyronova rovnice – výpočet rovnovážné teploty
V trojném bodě vody při teplotě 0,01 °C je rovnovážný tlak par 611
Pa. Vypočítejte teplotu tání
ledu za tlaku 10 MPa. K dispozici máte následující data pro vodu
v trojném bodě:
ΔtáníHm = 6,009 kJ mol−1,
ϱ(l) = 1 kg dm−3,
ϱ(s) = 0,917 kg dm−3.
Při výpočtu předpokládejte, že jak entalpie tání tak rozdíl molárních
objemů nezávisí na teplotě. Pro molární hmotnost vody použijte
zaokrouhlenou hodnotu 18 g mol−1.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
T2 = 272,42 K (t = 0,73 °C)
(ΔtáníVm = −1,629 . 10−3 dm3 mol−1)
Postup
Hustoty převedeme na molární objemy a pak aplikujeme Clapeyronovu rovnici.
Audio
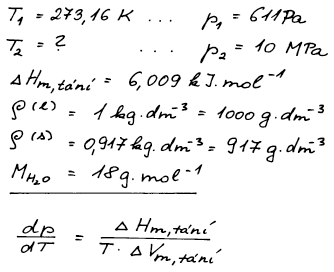
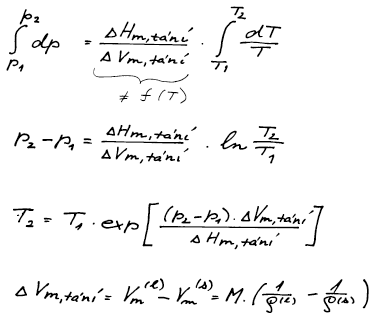
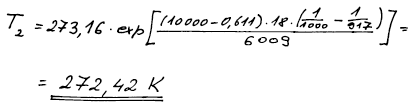
Jedná se o rovnováhu mezi kapalnou a tuhou fází (s–l). Na rovnovážné
křivce známe jeden bod 1 (p1,T1) a teplo (vyměněné za konstantního
tlaku = entalpii) fázového přechodu. Na této rovnovážné křivce chceme
spočítat bod 2 tj. p2 při T2 .
K výpočtu rovnováhy (s–l) využijeme Clapeyronovu rovnici.
Integrovaný tvar Clapeyronovy rovnice získáme integrací za
předpokladu, že poměr změny entalpie ku změně objemu tání je na
teplotě nezávislý.
U většiny látek teplota tání s tlakem nepatrně roste. Voda však tvoří
výjimku, protože při teplotě tání je hustota tuhé fáze menší než
hustota kapaliny.