1.6.2 Clausiova-Clapeyronova rovnice
Tlak nasycené páry ethylacetátu při t1 = 8,5 °C činí p1s = 5,33 kPa a při teplotě t2 = 41,4 °C je p2s = 26,66 kPa. Odhadněte tlak nasycené páry ethylacetátu při t3 = 85,6 °C.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
p3s = 145,63 (ΔvýpHm = 36 040 J mol−1)
Postup
Ze dvou známých bodů a integrovaného tvaru Clausiovy-Clapeyronovy rovnice vypočteme výparnou entalpii, kterou pak použijeme pro výpočet tlaku nasycených par při t3.
Audio
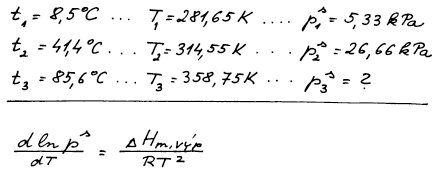
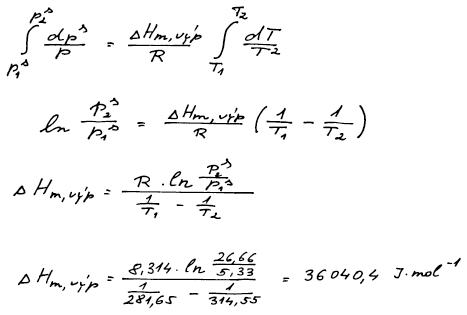
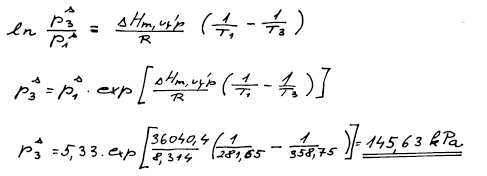
Máme rovnováhu mezi kapalnou a parní fází (l–g). Na rovnovážné křivce
známe dva body, (p1s,T1) a (p2s,T2). Ze
znalosti těchto dvou rovnovážných bodů si musíme nejprve vypočítat
teplo fázové přeměny – molární výparnou enthaplii. Potom již budeme
schopni vypočítat (ps,T) v jakémkoli bodě rovnováhy kapalina
– pára, tedy i v bodě 3.
Pro výpočet rovnováhy v jednosložkovém systému, kde se vyskytuje jedna
z fází pára, využíváme Clausiovu–Clapeyronovu rovnici. Při integraci
předpokládáme, že v našem relativně úzkém teplotním intervalu výparná
entalpie není funkcí teploty.
Nejprve z Clausiovy–Clapeyronovy rovnice ze znalosti bodů 1 a 2
vypočteme molární výparnou entalpii.
Tenzi par neboli tlak nasycených par v bodě 3 opět vypočteme pomocí
Clausiovy–Clapeyronovy rovnice, kde v tuto chvíli už známe výparnou
entalpii a jeden bod. Je jedno jestli si zvolíme bod 1 nebo 2.