1.9.1 Reakce nultého a prvního řádu – výpočet rychlostní konstanty a času
Reakce
![]()
proběhne za 45 minut ze třiceti procent. Za jak dlouho zreaguje 78% výchozí látky, je-li reakce (a) nultého, (b) prvního řádu?
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
(a) τ = 117 min, (b) τ = 191 min
Postup
Z integrovaného tvaru kinetické rovnice (zvlášť pro 0. a 1. řád) a z podmínky c(45min) = 0,70c(0) určíme rychlostní konstantu. Pak použijeme integrovaný tvar kinetické rovnice ještě jednou pro určení času z podmínky c(τ) = 0,22c(0).
Audio
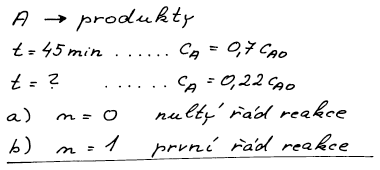
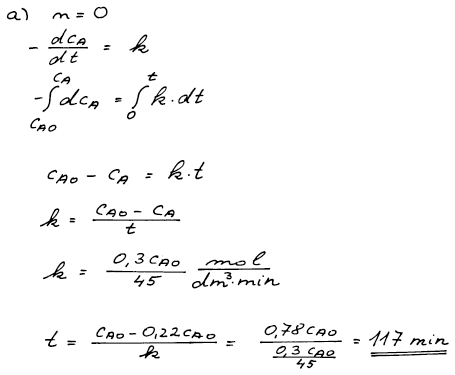
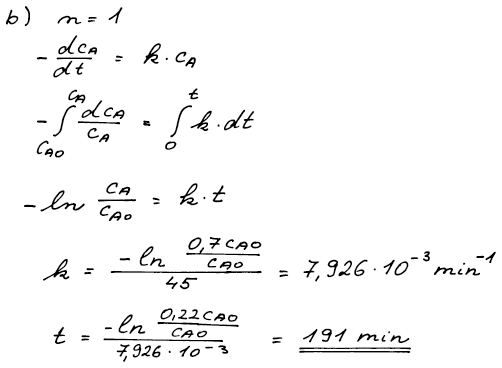
Za 45 minut reakce proběhla ze 30%. To znamená, že 70% původně přítomné látky A zůstalo v reaktoru nezreagováno a okamžitou koncentraci látky A vyjádříme jako cA = 0,7 cA0.
Z integrovaného tvaru kinetické rovnice nultého řádu v čase t = 45 min
si musíme nejprve vyjádřit rychlostní konstantu reakce. Ta je pro
danou teplotu konstantní, a tak ji můžeme využít pro výpočet času t,
kdy nastane situace, že 78%
původně přítomné látky A zreaguje.
Do integrovaného tvaru kinetické rovnice 1.řádu dosadíme údaje v čase
45 minut a vypočteme rychlostní konstantu reakce 1. řádu. Stejnou
kinetickou rovnici s takto vypočtenou rychlostní konstantou použijeme
k výpočtu času potřebného ke zreagování 78% látky A.