|
Regresní techniky v programu ERA
Počítačová aplikace pro regresní analýzu ERA (Easy Regression Analysis) byla vyvinuta s cílem poskytnout spolehlivé a uživatelsky jednoduché prostředí pro řešení všech typů regresních úloh, potřebných pro komplexní zpracování experimentálních dat z výzkumu chemické kinetiky. Zároveň byla do aplikace implementována řada funkcí, jejichž využití v aplikovaném výzkumu bude pravděpodobně poněkud omezenější, ale které jsou potřebné pro komplexní studium problému.
1. Použité algoritmy a jejich výběr
Numerické algoritmy byly vybírány především s ohledem na robustnost a spolehlivost aplikace. Rychlost výpočtu byla až sekundárním výběrovým kritériem, ačkoliv rozhodně nebyla opomíjena. Stejná kritéria byla uplatněna i při nastavení a doladění vlastností algoritmu. Uvedené preference vycházejí z filozofie aplikace, která se snaží odstínit uživatele od technických problémů spojených s výpočty a umožnit komplexní vyhodnocení dat sice ne bez základní znalosti regresní analýzy, ale bez požadavků na detailní znalost numerických metod a programování.
1.1 Výpočet účelové funkce
Program ERA podporuje několik účelových funkcí. Základní funkcí je prostý součet čtverců reziduálních odchylek, dále jeho modifikace ve formě váženého součtu. Matice vah nastavuje váhy automaticky na převrácenou hodnotu rozptylu odezvy. Rozptyly odezev jsou v uvedeném případě aproximovány jejich reziduálními rozptyly.
Pro případy s výraznou vzájemnou závislostí chyb v různých odezvách a měřeních s neznámou kovarianční maticí byl implementován Box-Draperův determinant SBD, počítaný podle vztahu
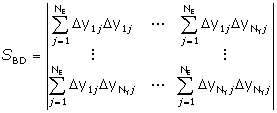
1.2 Optimalizační algoritmy pro odhad parametrů
Při volbě vhodného optimalizačního algoritmu pro extremalizaci účelové funkce bylo třeba vyjít z požadavků na jeho vlastnosti, odvozených od charakteru typicky řešených systémů. Nejdůležitějším požadavkem byla robustnost metody, myšlená především ve smyslu spolehlivé konvergence do globálního minima i z relativně vzdálených počátečních odhadů. Dalšími požadavky byla jednoduchost metody a univerzálnost jejího použití pro odlišné typy modelů. Cílem bylo především nastavení parametrů metody tak, aby byla použitelná na nejrůznější modely bez úprav a změn nastavení i za cenu mírného snížení rychlosti kovergence. Rychlost metody byla proto až třetím kritériem výběru. Optimalizační algoritmus pro program ERA byl z výše uvedených důvodů hledán ve skupině stochastických optimalizačních metod.
1.2.1 Optimalizační algoritmus ERA
Optimalizační algoritmus ERA je modifikací metody Gaines-Gaddy, která má pro účely odhadu kinetických parametrů nejvyváženější vlastnosti. Hlavní výhodou uvedeného typu metod je vysoká odolnost proti lokálním extrémům při zachování velmi vysoké konvergence do blízkosti globálního optima.
Optimalizační algoritmus programu ERA definuje prohledávanou oblast jako m‑rozměrný hyperelipsoid s velikostmi poloos proporcionálními ke složkám nejlepší aproximace vektoru parametrů podle vztahu
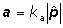
kde a je vektor poloos hyperelipsoidu a ka konstanta úměrnosti (viz. obr. 1). Pro případ odhadu parametrů, které nabývají pouze kladných hodnot (je známo zda je parametr kladný nebo záporný), což platí pro většinu aplikací v kinetice, byla na základě testů stanovena optimální hodnota konstanty ka » 0.5. Uvedená hodnota postačuje pro spolehlivou konvergenci do globálního optima a umožňuje vysokou konvergenční rychlost. Pro odhad parametrů s neznámým znaménkem je potřebná hodnota podstatně vyšší (ka » 4).
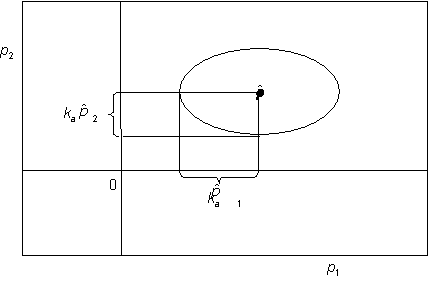
Obr. 1 – Definice prohledávané oblasti algoritmu ERA
Poloha náhodného výběru uvnitř prohledávané oblasti je určena jednotkovým pseudonáhodným směrovým vektorem v a normalizovanou vzdáleností l od aproximace 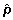 . Vzdálenost l je pseudonáhodné číslo určené vztahem . Vzdálenost l je pseudonáhodné číslo určené vztahem
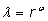
Ze vztahu předchozího je patrné, že parametr w musí být z intervalu á0;1), aby byly preferovány výběry z okraje prohledávané oblasti a z intervalu (1;¥) pro preferenci výběrů umístěných blíže k jejím středu. Plynulý nárůst hodnoty parametru w je zajištěn jeho výpočtem ze vztahu
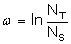
kde NT představuje celkový počet vyčíslených náhodných výběrů z prohledávané oblasti a NS počet těch, které byly úspěšné (vedly ke snížení hodnoty účelové funkce). Výslednou iterační formuli pro algoritmus ERA lze pro k-tý parametr shrnout do následujícího vztahu
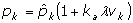
Vývojový diagram optimalizačního algoritmu ERA je znázorněn na obr. 2.
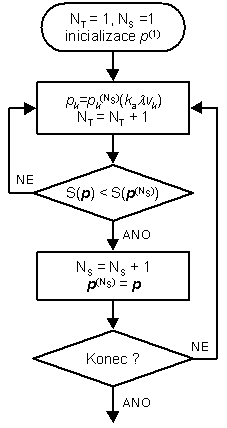
Obr. 2 – Vývojový diagram algoritmu optimalizačního ERA
Algoritmus ERA konverguje spolehlivě a velmi rychle ke globálnímu optimu až do relativní přesnosti pohybující se okolo 0.1 % a poté rychlost konvergence dosti prudce klesá. Protože chyba způsobená nepřesností experimentálních dat je u typicky zpracovávaných systémů podstatně větší než chyba odhadu způsobená předčasně ukončenou optimalizací, je většinou možné ukončit výpočet ještě ve fázi rychlé konvergence. Další možností zlepšení konvergence je použití jiné metody pro jemné dokonvergování. Vzhledem k tomu, že pro tyto účely již není vhodné vybírat ze stochastických metod, byla implementována Nelder-Meadova modifikace simplexové metody, která využívá posledních m+1 (kde m je počet odhadovaných parametrů) aproximací pro inicializaci simplexu.
Další výhodou algoritmu je relativně malá velikost prohledávaného okolí v kombinaci s jeho posunem okamžitě po nalezení lepší aproximace. Uvedené vlastnosti jsou velmi vhodné v případě, kdy jsou k dispozici pouze velmi přibližné počáteční odhady některých parametrů. Jiné metody, zejména LJ, vykazují výrazné snížení rychlosti konvergence v případě, kdy je velikost prohledávané oblasti v nějakém směru podstatně menší než její vzdálenost od optima. Zvětšení prohledávané oblasti je nutno obvykle kompenzovat zvýšením počtu výběrů v každém iteračním bloku, takže zvýšení rychlosti konvergence příliš nenapomáhá. Pro zvýšení spolehlivosti konvergence do globálního optima je významný i způsob zmenšování rozptylu výběrů okolo nejlepší aproximace, místo změny velikosti prohledávané oblasti.
1.3 Hodnocení spolehlivosti
Pro hodnocení spolehlivosti parametrů byl implementován výpočet konfidenčních intervalů a průmětů konfidenční oblasti do parametrických os (konfidenční meze).
1.3.1 Konfidenční intervaly a korelační koeficienty
Konfidenční interval (interval spolehlivosti) La(pk) pro parametr pk je definován vztahem
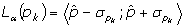
kde spkpředstavuje směrodatnou odchylku parametru, 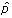 optimální hodnotu parametru a a zvolenou hladinu významnosti. Směrodatná odchylka parametru je určena z rovnice optimální hodnotu parametru a a zvolenou hladinu významnosti. Směrodatná odchylka parametru je určena z rovnice
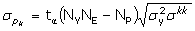
kde t je kritická hodnota Studentova rozdělení pro hladinu významnosti a a (NYNE – NP) stupňů volnosti a skk k-tý diagonální prvek variačně‑kovarianční matice parametrů S. V praxi obvykle není k dispozici dostatečné množství opakovaných experimentů (jsou-li nějaké) pro určení rozptylu závisle proměnné. Rovněž velice zřídka je možné určit její rozptyl z předchozí zkušenosti, protože je ovlivňován mnoha faktory, závisícími na zkoumaném systému i experimentátorovi. Proto se nejčastěji používá odhad rozptylu z reziduálního rozptylu sR2 podle vztahu
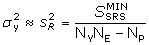
kde 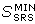 je součet čtverců reziduálních odchylek v optimu. je součet čtverců reziduálních odchylek v optimu.
Šířka konfidenčního intervalu odhadnutého parametru závisí na příslušném diagonálním prvku kovarianční matice parametrů. Její výpočet používá pouze první derivace modelu podle parametrů, takže vyšší stupeň závislosti modelu na parametrech se do hodnot jejích prvků nepromítne. Šířku konfidenčního intervalu proto neurčuje přímo model, ale jeho aproximace Taylorovými rozvoji prvního stupně v okolí optimálních hodnot parametrů. Proto jsou konfidenční intervaly parametru symetrické, se středem v optimální hodnotě parametru. Z uvedeného způsobu výpočtu a vlastností vyplývají následující omezení pro použití konfidenčních intervalů:
² Konfidenční interval je schopen přesně indikovat spolehlivost parametru, pokud je model vůči němu lineární.
² V případě nelineárního modelu je intervalový odhad pouze natolik přesný, nakolik je přesná aproximace modelu Taylorovým rozvojem 1. stupně. Proto konfidenční interval není vhodným kritériem spolehlivosti parametrů, vůči kterým vykazuje model silně nelineární chování.
² Aproximace Taylorovým rozvojem je tím méně přesná, čím se provádí na širším intervalu. Proto i u poměrně málo nelineárních modelů mohou být konfidenční intervaly značně zkreslené, pokud jsou široké (malé množství dat, nepřesná data).
Konfidenční intervaly se jako kritéria spolehlivosti vyskytují v největší části prací.
Konfideční intervaly pro jednotlivé parametry se počítají podle explicitních vztahů [6, 7]. Rozptyl závisle proměnných potřebný pro výpočet směrodatné odchylky parametru je možno dodat jako externí informaci. V opačném případě je odhadnut z hodnoty součtu čtverců reziduálních odchylek podle vztahu [8]. Variačně‑kovarianční matice S se vypočítá podle vztahu
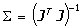
kde J je Jacobiho matice definovaná vztahem [12]. Variačně‑kovarianční matice je čtvercová a symetrická s rozměrem odpovídajícím počtu parametrů. Je možno ji normalizovat tak, aby její diagonální prvky byly jednotkové podle vzorce
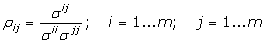
kde prvky r jsou prky normalizované (korelační) matice R. Nediagonální prvek korelační matice rij vyjadřuje normalizovanou kovarianci mezi i‑tým a j‑tým parametrem (korelační koeficient) z intervalu á‑1;1ñ. Nabývá‑li korelační koeficient hodnoty 0 parametry pi a pj je možno odhadnout s přesností odpovídající kvalitě experimentálních dat. Čím větší je absolutní hodnota korelačního koeficientu, tím menší vliv má změna hodnoty jednoho z parametrů na hodnotu účelové funkce, protože tato změna může být ve větší míře kompenzována změnou hodnoty druhého parametru. V případě, že korelační koeficient nabývá marginální hodnoty z intervalu á‑1;1ñ jsou parametry zcela korelovány a jejich hodnoty nelze určit separátně.
1.3.2 Konfidenční oblast a konfidenční meze
Konfidenční oblast lze definovat jako takový podprostor v NP-rozměrném prostoru parametrů, ve kterém se na zvolené hladině významnosti a nalézají skutečné hodnoty parametrů. Konstrukce jejího přibližného tvaru, za předpokladů platných pro výpočet konfidenčních intervalů, vede k NP-rozměrnému (hyper)elipsoidu se středem v místě, jehož souřadnice odpovídají optimálním hodnotám parametrů. Skutečný tvar konfidenční oblasti se však u nelineárních modelů může od elipsoidu do značné míry lišit, stejně jako jeho velikost. V některých případech může být konfidenční oblast i nekonvexní.
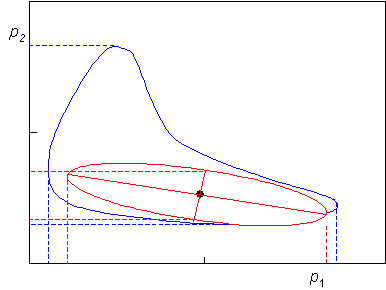
Obr. 3 – Porovnání skutečného tvaru řezu konfidenční oblasti(––) s jeho eliptickou aproximací(--) pro nelineární model. Čárkovaně jsou vyznačeny charakteristické rozměry – konfidenční interval (---) a průmět konfidenční oblasti (---)
Obrázek 3 ukazuje porovnání dvourozměrného řezu konfidenční oblastí s její eliptickou aproximací pro nelineární model. Charakteristickým rozměrem idealizované konfidenční oblasti jsou délky jejích os, které odpovídají šířkám konfidenčních intervalů [6]. V případě výrazně odlišného tvaru skutečné a idealizované konfidenční oblasti lze použít místo konfidenčních intervalů charakteristické rozměry skutečné konfidenční oblasti. Jsou jimi průměty konfidenční oblasti do parametrických os.
Skutečnou konfidenční oblast je možné definovat jako množinu bodů v parametrickém prostoru, pro které platí nerovnost
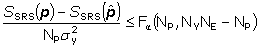
kde F je kritická hodnota Fischerova rozdělení pro hladinu významnosti a a NP a NYNE – NP stupňů volnosti. Pro hranici (povrch) konfidenční oblasti platí vztah [11] ve formě rovnosti. Konfidenční oblasti jsou vhodné spíše pro grafickou interpretaci a následné vizuální hodnocení. Jelikož je žádoucí mít k dispozici kritérium intervalové povahy, ale nezatížené nedostatky konfidenčních intervalů, implementuje program ERA velmi důležitou funkci výpočtu konfidenčních mezí.
Konfidenční meze jsou definovány jako průměty obrysu skutečné konfidenční oblasti, zkonstruované pro požadovanou hladinu spolehlivosti podle vztahu [11], do os parametrů. Na rozdíl od intervalů spolehlivosti nemusí být interval určený konfidenčními mezemi symetrický podle optimální hodnoty parametru, jak ukazuje obr. 4.
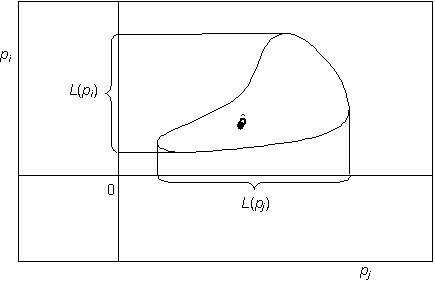
Obr. 4 – Definice konfidenčních mezí podle skutečné konfidenční oblasti
Výpočet konfidenčních mezí vychází stejně jako v případě konfidenční oblasti ze vztahu [11] pro kritérium věrohodnostního poměru. Protože uvedený vztah platí pro všechny body p náležící do konfidenční oblasti, je za předpokladu její spojitosti pro určení konfidenčních mezí zapotřebí hledat maximální a minimální hodnoty parametrů, které kritériu vyhovují.
1.4 Významnost parametrů
Vzhledem k omezené přesnosti a množství experimentálních dat se některé parametry mohou ukázat jako statisticky nevýznamné. Rovněž mohou být na uvažované hladině významnosti nevýznamně odlišné od nějaké hodnoty, která svým fyzikálním významem umožňuje zásadní zjednodušení modelu. Typické příklady jsou následující:
² rychlostní konstanta » 0 (daná reakce neprobíhá významnou rychlostí)
² řád reakce » 1 (reakci lze aproximovat jako nekatalyzovanou)
² adsorpční koeficient » 0 (sorpce látky je zanedbatelná)
Nevýznamné parametry je nutno z modelu vyloučit, protože zvýšením stupňů volnosti, případně korelací, mohou výrazně ovlivnit spolehlivost ostatních parametrů.
Parametr je možné považovat za statisticky nevýznamný na uvažované hladině významnosti od dané hodnoty, pokud tato hodnota leží uvnitř jeho intervalového odhadu vypočítaného pro tuto hladinu významnosti. Prostý konfidenční interval pro řadu nelineárních modelů není dostatečně vhodný k testům významnosti pro svou středovou symetrii vzhledem k optimální hodnotě parametru. Typický tvar konfidenční oblasti pro Langmuir-Hinshelwoodovy modely (a pravděpodobně pro řadu dalších modelů, v nichž záporné hodnoty parametrů nemají fyzikální význam) je kapkovitý. Přitom její pološířka v kladném směru je často velmi podstatně větší než ve směru záporném, jak ukazuje obrázek 5.
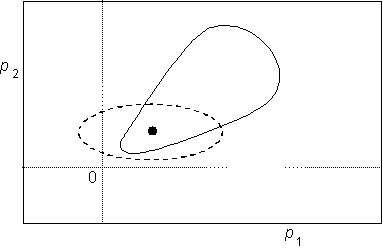
Obr. 5 – Typický tvar konfidenční oblasti u Langmuir-Hinshelwoodových modelů
Obrázek ukazuje typický případ, kdy konfidenční interval indikuje parametr p1 jako nevýznamný, ačkoliv je skutečnost reprezentovaná konfidenční oblastí jiná.
1.5 Testy autokorelace
Pro účely testování normality rozložení reziduí existuje řada testových statistik. ERA implementuje autokorelační test založený na Neumannově statistice namísto běžnějšího Durbin‑Watsonova testu, protože Neumannova statistika je vhodnější pro případy s menším množstvím měření na jednotlivých odezvách, a proto lépe vyhovuje zaměření aplikace.
2. Koncepce regresního modelu
Povaha kinetických modelů vyžaduje, aby program umožnil práci s modely tvořenými soustavou algebraických a obyčejných diferenciálních rovnic prvního řádu. Přitom používané algebraické rovnice jsou vždy explicitní vzhledem k jedné ze závisle proměnných, stejně jako rovnice diferenciální vzhledem k její derivaci.
Pro řešení soustav obyčejných diferenciálních rovnic byla použita Adams-Moultonova prediktor-korektor metoda. Vzhledem k tomu, že analytické vyjádření derivací účelové funkce a reziduí podle parametrů nemusí být obecně možné (např. v případě, že neexistuje analytický vztah pro výpočet účelové funkce a reziduí, protože diferenciální rovnice v modelu nejsou analyticky řešitelné), provádějí se veškeré nezbytné výpočty derivací numericky, diferenčními formulemi. Počet bodů použitých pro diferenční formuli a velikost jejího kroku je optimalizována s ohledem na přesnost integrační metody.
Výsledkem řešení modelu je matice YM, která obsahuje hodnoty závisle proměnných vypočítaných modelem pro hodnoty parametrů p v bodech měření definovaných řádky matice XE,
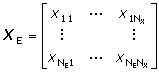 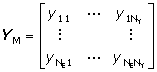
Matice YM po odečtení od matice naměřených hodnot závisle proměnných YE se stejnou strukturou poskytne matici reziduí DY. Pomocí diferenčních formulí se též vypočítá Jacobiho matice parciálních derivací reziduí podle regresních parametrů J
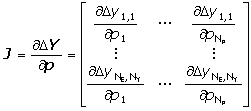
2.1.1 Překlad a dynamické připojení modelu
Rovnice matematického modelu jsou v programu ERA chápány jako funkce (ve smyslu programovacího jazyka), do které se jako vstupní parametry předají vektory nezávisle proměnných, závisle proměnných a parametrů. Funkce vrátí jako výstup nový vektor závisle proměnných, případně jejich derivací, obsahuje‑li model diferenciální rovnice. Popsaná funkce přitom není integrální součástí programu, ale překládá se zcela nezávisle na vlastním programu. Výsledkem překladu je knihovna, kterou lze za běhu programu připojit k vlastnímu programu tak, že ten následně může obsaženou funkci používat, jako kdyby byla jeho integrální součástí.
Program ERA 3.0 dále zjednodušuje práci s modely tím, že automaticky provádí nejen překlad a připojení knihovny modelu, ale generuje i její zdrojový kód na základě rovnic zadaných uživatelem, který proto nemusí zadávat nic jiného než vlastní modelové rovnice, případně deklarovat použité pomocné proměnné. Zadávání se provádí v nejjednodušší možné formě prostřednictvím mezisyntaxe. Následující ukázka obsahuje zadání modelu, ze kterého je programem vygenerován výše uvedený zdrojový kód knihovny modelu
language = pascal
declar
r1,r2,r3,ads : Double;
end declar
static
end static
dynamic
ads := 1 + p[4]*y[1] + p[5]*y[2] + p[6]*y[3];
r1 := p[1]*p[4]*y[1]/ads;
r2 := p[2]*p[5]*y[2]/ads;
r3 := p[3]*p[5]*y[2]/ads;
dy[1] := -r1 + r3;
dy[2] := r1 - r2 - r3;
dy[3] := r2;
end dynamic
Program je schopen na základě zadání modelu vygenerovat zdrojový kód v jazyce Pascal. K vlastnímu překladu se poté použije externí překladač, který není součástí instalace programu, programu je při instalaci pouze zadáno jeho umístění na počítači.
3. Seznam symbolů
Latinské symboly
a vektor poloos hyperelipsoidu definujícího prohledávanou oblast -
B diagonální matice s prvky bjj = |hjj|-½ (pro hjj = 0 je bjj = 1) –
C variačně-kovarianční matice parametrů –
F kritická hodnota Fischerova rozdělení –
H matice druhých derivací účelové funkce (Hessián) –
J Jacobiho matice parciálních derivací reziduí podle parametrů –
k rychlostní konstanta chemické reakce min-1
konstanta úměrnosti –
K formální adsorpční koeficient –
L věrohodnostní funkce –
konfidenční interval –
M momentová matice (prvky mij) –
NE počet měření –
NP počet parametrů –
NS počet úspěšných náhodných výběrů -
NY počet závisle proměnných (odezev) –
p hustota pravděpodobnosti –
p vektor parametrů -
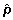 vektor optimálních hodnot parametrů – vektor optimálních hodnot parametrů –
q gradient účelové funkce –
r rychlost chemické reakce min-1
délka kroku optimalizační metody –
r krok optimalizační metody –
r' rychlost zpětné reakce min-1
R korelační matice (prvky rij) –
definiční matice gradientové metody (pozitivně definitní) –
sR2 reziduální rozptyl –
S účelová funkce –
t kritická hodnota studentova rozdělení –
t čas min
v směrový vektor –
XM matice bodů měření -
y vektor závisle proměnných –
Dy reziduum –
Y matice naměřených hodnot závisle proměnné –
Z diagonální matice -
Řecké symboly
e kontrakční koeficient -
e kontrakční vektor -
k kladná konstanta rychlosti konvergence -
l kladná konstanta -
m vektor středních hodnot náhodné veličiny –
n stechiometrický koeficient –
rij korelační koeficient –
q stupeň pokrytí povrchu –
s2 rozptyl parametru –
sy2 rozptyl závisle proměnné, rozptyl měření –
 kovarianční matice chyb odhadu parametrů (prvky sij) – kovarianční matice chyb odhadu parametrů (prvky sij) –
 y kovarianční matice chyb měření (prvky syij) – y kovarianční matice chyb měření (prvky syij) –
w parametr hustoty rozdělení náhodných výběrů -
| 
