|
Řešené příklady
Příklad 1: Jednoduchá nelineární regrese
Zadání:
Odhadněte optimální hodnotu rychlostní konstanty reakce prvního řádu dané následující rovnicí:
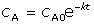 [13] [13]
Použijte data z následující tabulky:
| t, min | 0 | 5 | 10 | 15 | 20 | 25 | 30 | | cA | 100 | 85 | 61 | 52 | 34 | 25 | 24 |
Řešení:
V rámci tohoto jednoduchého příkladu bude vyřešena základní regresní úloha. Vzhledem k tomu, že se jedná o úvodní příklad bude postup řešení doplněn o podrobný postup obsluhy programu ERA, použitý pro jeho řešení. Matematický model definovaný rovnicí [13] je třeba zadat do programu ERA v syntaxi a symbolice popsané v kapitole 7.1. Zápis modelu bude tedy mít následující formu:
language=pascal
declar
end declar
static
end static
dynamic
y[1] := 100*exp(-p[1]*x[1]);
end dynamic
Zápis modelu naznačuje, že řešený problém zahrnuje jednu nezávisle proměnnou (čas, t), jednu závisle proměnnou (koncentrace, cA) a jeden parametr (rychlostní konstanta, k). Model je tvořen jedinou algebraickou rovnicí a soubor experimentálních dat obsahuje 7 měření. Informace o rozměru řešeného systému je třeba vyplnit do karty Dimensions (viz kap. 6.3.1) a data do tabulky dat, jak ukazují následující obrázky.
 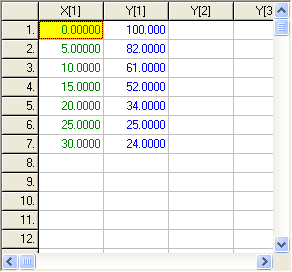
Zadaná data je možno uložit do souboru, zatímco model je nutno uložit a zkompilovat (viz kap. 7.2).
Po specifikaci modelu a experimentálních dat může být účelné přepnout zobrazení sešitu nastavení na kartu Parameters a zobrazení hlavního sešitu na kartu Fitchart tak, jak je naznačeno na následujícím obrázku.
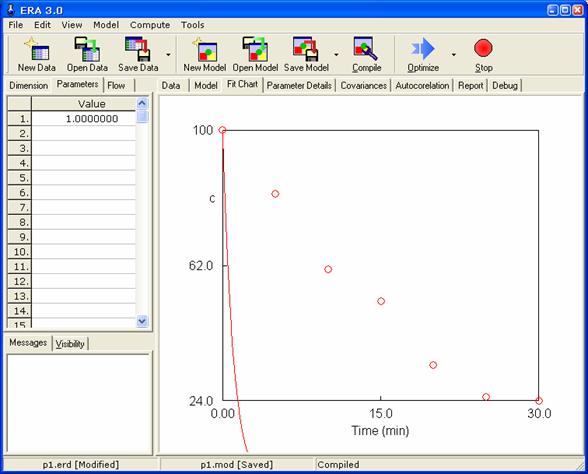
Počáteční nastavené hodnoty parametrů (v tomto případě pouze jediného parametru) jsou uvedeny na kartě Parameters. Těmto hodnotám (hodnotě) odpovídá křivka patrná na obrázku v kartě Fitchart. Body na obrázku reprezentují zadaná experimentální data. Změníme-li hodnotu parametru, dojde ihned i ke změně grafického znázornění řešení modelu tak, aby odpovídalo aktuální hodnotě parametru. Ukázku změny zahrnuje následující obrázek
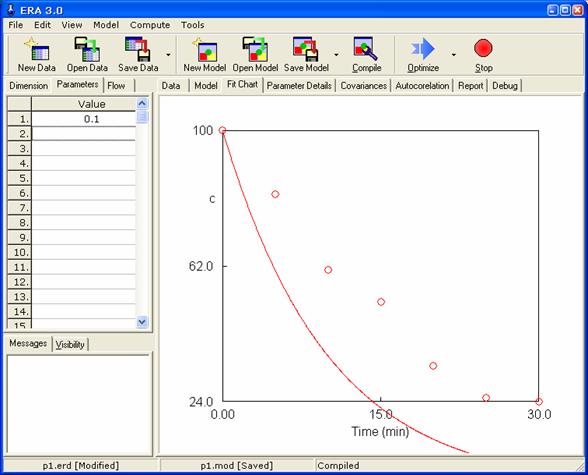
Cílem odhadu optimálních hodnot parametrů (v tomto případě rychlostní konstanty) je nalezení takové jeho hodnoty, která minimalizuje hodnotu účelové funkce – je vzhledem k experimentálním datům nejpravděpodobnější. V programu ERA toho lze dosáhnout spuštěním optimalizace tlačítkem Optimize na panelu nástrojů nebo volbou menu Compute/Optimize. Optimalizační hodnota poté iteračně mění hodnoty parametrů tak, aby minimalizovala hodnotu účelové funkce. Výpočet je možné kdykoliv ukončit tlačítkem Stop na panelu nástrojů a případně znovu spustit opětovným stiskem tlačítka Optimize. Tak, jak se v průběhu výpočtu nalézají lepší aproximace řešení, aktualizují se hodnoty parametrů, grafické zobrazení i minimální dosažená hodnota účelové funkce zobrazovaná na kartě Flow v sešitu nastavení. Na ní je rovněž možné typ účelové funkce změnit na libovolný typ podle kapitoly 1.1. Poté, co je dosaženo požadované přesnosti aproximace řešení (kdy se již zobrazovaná hodnota účelové funkce nemění nebo se mění jen velmi málo) je třeba výpočet vždy ukončit stiskem tlačítka Stop. Ukázku stavu programu po ukončení optimalizace představuje následující obrázek.
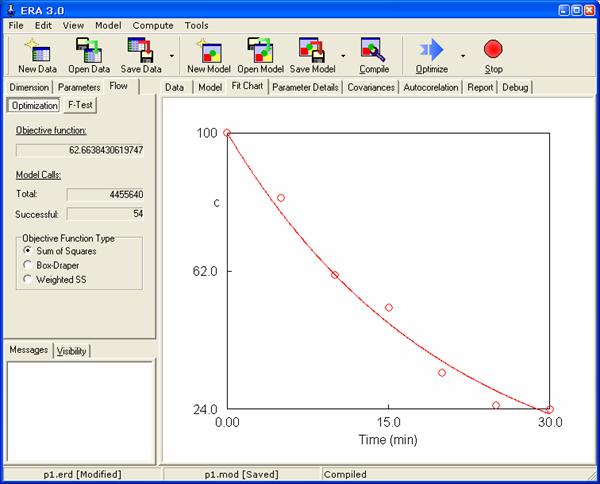
Výsledný graf proložení (fitchart) je možné vyexportovat do souboru stiskem pravého tlačítka myši kdekoli na obrázku a výběrem položky Export ze zobrazivšího se kontextového menu. Odhadnuté hodnoty parametrů lze nalézt na kartách Parameters nebo Parameter Details jak znázorňuje následující obrázek.
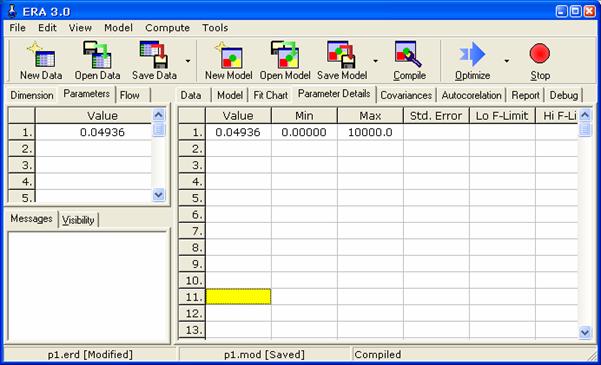
Výsledek:
Optimální hodnota rychlostní konstanty k, odhadnutá z experimentálních dat je 0,04936. Pro tuto hodnotu byla dosažena minimální hodnota součtu čtverců reziduálních odchylek S = 62,66.
Příklad 2: Jednoduchá nelineární regrese s diferenciální rovnicí
Zadání:
Odhadněte optimální hodnotu rychlostní konstanty reakce prvního řádu z dat použitých v předchozím příkladu. Tentokrát jako model použijte diferenciální rovnici:
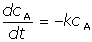 [14] [14]
Zhodnoťte spolehlivost odhadnuté rychlostní konstanty s použitím konfidenčního intervalu a konfidenčních mezí.
Řešení:
Postup první části řešení je velmi podobný předchozímu příkladu. Byl-li soubor experimentálních dat již vytvořen, není nutné zadávat data znovu, ale je možné je tento soubor otevřít volbou menu File/Open Data File nebo tlačítkem Open Data na panelu nástrojů. Zápis modelu bude mít následující formu:
language=pascal
declar
end declar
static
end static
dynamic
dy[1] := -p[1]*y[1];
end dynamic
Počáteční podmínka nutná pro řešení diferenciální rovnice se vezme automaticky z prvního řádku experimentálních dat. Vzhledem k tomu, že model nyní obsahuje diferenciální rovnici namísto algebraické, je třeba upravit i nastavení na kartě Dimensions podle následujícího obrázku.

Model je třeba uložit a zkompilovat až po nastavení rozměru řešeného problému. Odhad optimální hodnoty parametru je zcela stejný jako v předchozím příkladě a stejné jsou rovněž dosažené výsledky. Není to překvapující protože se jedná o stejná data a stejný model, i když v diferenciálním tvaru.
Po spuštění a zastavení optimalizace můžeme přistoupit k výpočtu intervalových odhadů parametrů pro hodnocení jejich spolehlivosti. Konfidenční interval (viz kap. 1.3.1) spočítáme volbou menu Compute/Standard Errors. Výsledky se objeví na kartě Parameter Details ve sloupci Std. Error. Jedná se o poloviční šířku konfidenčního intervalu, který je tedy podle následujícího obrázku 0,4936±0,00683 neboli á0,4253; 0,5619ñ.
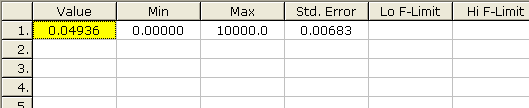
Konfidenční meze (viz kap. 1.3.2) lze spočítat volbou menu Compute/All F-Limits. Na rozdíl od předchozího výpočtu se jedná o výpočet iterativní, takže může trvat delší dobu. Průběžné výsledky se zobrazují v příslušných sloupcích na kartě Parameter Details. Výpočet je ukončen poté, co se objeví zpráva zachycená na následujícím obrázku. Na něm je rovněž vidět, že interval konfidenčních mezí pro rychlostní konstantu je á0,4442; 0,5446ñ.
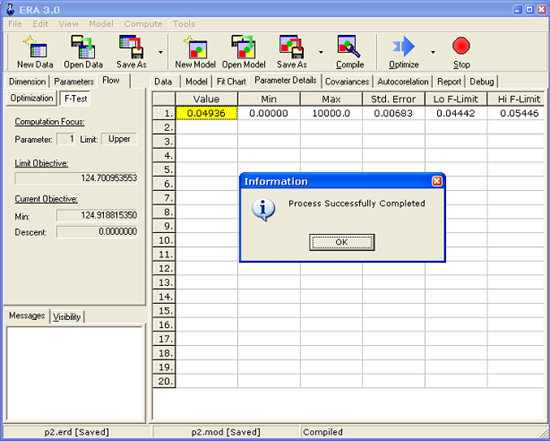
Výsledek:
Optimální hodnota rychlostní konstanty k, odhadnutá z experimentálních dat je 0,04936. Konfidenční interval je á0,4253; 0,5619ñ, interval konfidenčních mezí á0,4442; 0,5446ñ.
Příklad 3: Vícenásobná nelineární regrese
Zadání:
Ve vsádkovém reaktoru byla sledována jednoduchá reakce 1. řádu A ® B měřením koncentrace látky A při různých teplotách. Výsledky měření shrnuje tabulka.
| t, min | cA, % | | T = 303,15 K | T = 313,15 K | T = 323,15 K | | 0 | 102,0 | 98,3 | 96,9 | | 5 | 96,0 | 82,2 | 61,7 | | 10 | 83,9 | 53,8 | 31,0 | | 20 | 64,1 | 38,9 | 7,6 | | 50 | 32,8 | 12,3 | 1,2 | | 100 | 17,5 | 1,4 | 2,2 |
Jako model použijte diferenciální rovnici:
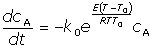 [15] [15]
kde k0 je rychlostní konstanta při teplotě T0 = 313,15 K, E aktivační energie a R plynová konstanta. Odhadněte optimální hodnoty parametrů a vypočítejte jejich intervalové odhady.
Řešení:
Při vícenásobné regresi zkoumáme závislost závisle proměnné na několika nezávisle proměnných současně, v tomto případě na čase a teplotě. Pro správnou funkci programu ERA musíme data uspořádat určitým způsobem. V první řadě je třeba správně nastavit rozměr problému na kartě Dimensions.

Integrace obyčejných diferenciálních rovnic se provádí automaticky podle první nezávisle proměnné. Proto v prvním sloupci matice dat musí být čas. Na druhou nezávisle proměnnou – teplotu – zbývá druhý sloupec. Protože model obsahuje diferenciální rovnici, musí být data seskupena podle stejných hodnot nezávisle proměnných kromě proměnné X[1] a v rámci těchto skupin seřazena podle X[1]. Důvodem je to, že pro každou skupinu dat je třeba zvolit počáteční podmínku. Pro tento příklad by matice dat měla vypadat následovně:
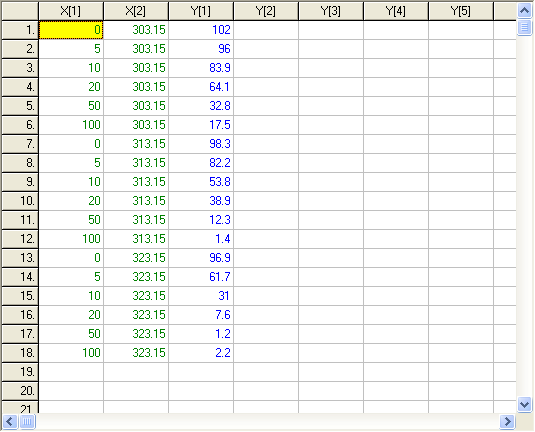
Přepis modelu do syntaxe používané programem ERA představuje následující ukázka:
language=pascal
declar
end declar
static
end static
dynamic
dy[1] := -p[1]*exp(p[2]*(x[2]-313.15)/(8.314*x[2]*313.15))*y[1];
end dynamic
Zkusme nyní nastavit počáteční hodnoty parametrů na p[1]=0,05 a p[2]=10000, a poté se podívat na grafické znázornění experimentálních dat a řešení modelu (viz následující obrázek).
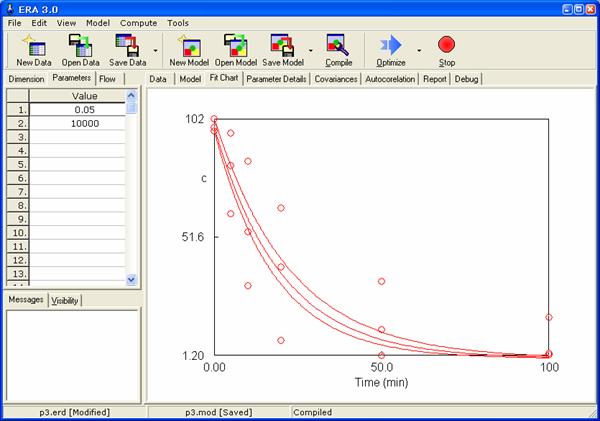
Zde je zřejmé, že program automaticky rozštěpí řešení do 3 větví pro jednotlivé teploty. Není-li zřetelně rozpoznatelné, který bod patří ke které větvi, je možné zapnout funkci číslování větví Tools/Preferences/Toggles/Show Branch Numbers (pro správnou funkci je třeba nastavit vyplněné body – viz kap. 6.1.6). Po spuštění dospěje optimalizace do stavu, který zachycuje následující obrázek
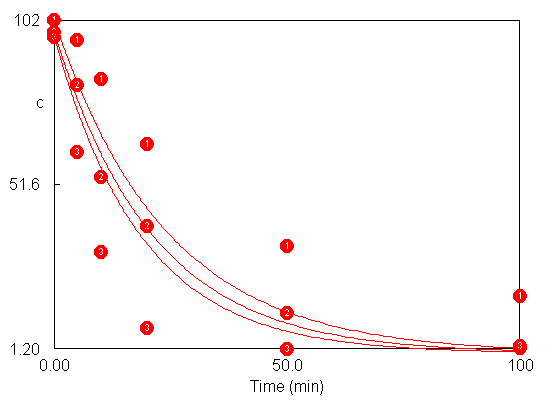
Příčinu předčasného ukončení optimalizace lze nalézt na kartě Parameter Details v hlavním sešitě (viz obrázek).

Hodnota aktivační energie (p[2]) zobrazená červeně dosáhla hranice intervalu povolených hodnot, který je pro každý parametr implicitně nastaven na á0; 10000ñ. K dokončení optimalizace je třeba povolený interval rozšířit, tzn. nastavit horní hranici např. na 106. Poté již optimalizačnímu algoritmu nic nebrání v dosažení optima. Následující obrázek znázorňuje porovnání vypočtených a naměřených dat.
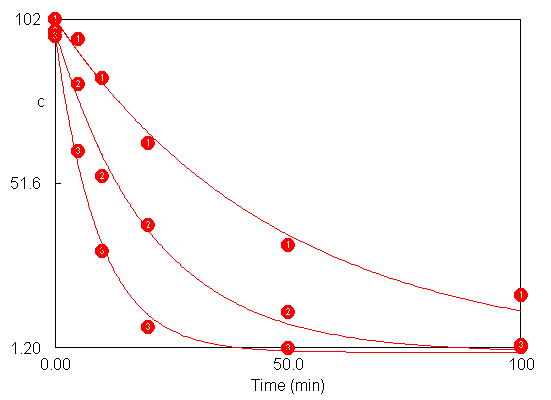
Intervalové odhady se vypočtou příkazy Compute/Standard Errors a Compute/All F-Limits analogicky jako v předchozím příkladě (viz následující obrázek).
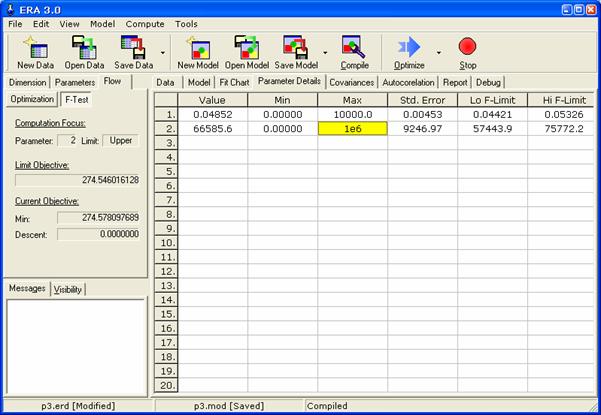
Výsledek:
Optimální hodnoty rychlostní konstanty k0 a aktivační energie E odhadnuté z experimentálních dat jsou 0,049±0,005 a 67000±9000 (chyba zaokrouhlena na první platné místo a hodnota zaokrouhlena podle řádu chyby). Intervaly konfidenčních mezí jsou á0,4421; 0,05326ñ a á57444; 75772ñ.
Příklad 4: Víceodezvová nelineární regrese a korelace parametrů
Zadání:
Ve vsádkovém reaktoru byla sledována následná heterogenně katalyzovaná reakce A ® B ® C ® D. Změřené hodnoty závislosti koncentrace na čase jsou uvedeny v tabulce včetně počátečních koncentrací (počátečních podmínek)
| t, min | 0 | 10 | 14 | 19 | 24 | 34 | 69 | 124 | | cA | 0.1012 | 0.0150 | 0.0044 | 0.0028 | 0.0029 | 0.0017 | 0.0003 | 0.0001 | | cB | 0.2210 | 0.1064 | 0.0488 | 0.0242 | 0.0015 | 0.0005 | 0.0004 | 0.0002 | | cC | 0.6570 | 0.6941 | 0.6386 | 0.5361 | 0.3956 | 0.2188 | 0.0299 | 0.0001 | | cD | 0.0208 | 0.1977 | 0.3058 | 0.4444 | 0.6055 | 0.7808 | 0.9680 | 0.9982 |
Jako model použijte soustavu diferenciálních rovnic sestavenou s použitím následujících rychlostních rovnic:
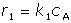 [16-a] [16-a]
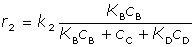 [16-b] [16-b]
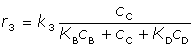 [16-c] [16-c]
Odhadněte optimální hodnoty parametrů, vypočítejte jejich intervalové odhady a korelační koeficienty. Porovnejte oba typy intervalových odhadů v souvislosti s hodnotami korelačních koeficientů.
Řešení:
Při víceodezvové regresi zkoumáme závislost několika závisle proměnných na jedné nebo několika nezávisle proměnných. Jako obvykle je při řešení příkladu programem ERA zapotřebí nejprve specifikovat rozměr systému a zadat experimentální data (viz obrázek).
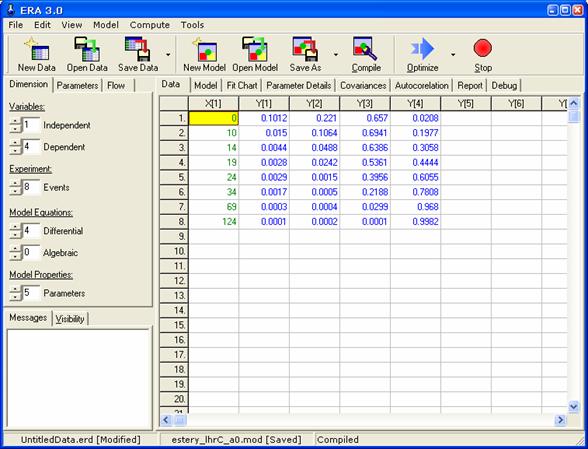
Matematický model bude mít následující tvar:
language=pascal
declar
r1,r2,r3,ads : Double;
end declar
static
end static
dynamic
ads := p[4]*y[2] + y[3] + p[5]*y[4];
r1 := p[1]*y[1]/ads;
r2 := p[2]*p[4]*y[2]/ads;
r3 := p[3]*y[3]/ads;
dy[1] := - r1;
dy[2] := r1 - r2;
dy[3] := r2 - r3;
dy[4] := r3;
end dynamic
V zápise modelu je vidět, že pro přehlednost i efektivitu zápisu je užitečné si definovat pomocné proměnné.
Optimalizace již u tohoto komplexnějšího modelu trvá déle a její doba se může pohybovat od několik sekund do minuty podle zvolených počátečních hodnot parametrů. Pro zajímavost je možné porovnat rychlost konvergence z různých počátečních hodnot parametrů – tzv. počátečních odhadů.
| i | Optimalizace probíhá několikanásobně rychleji, nemusí-li program zobrazovat grafické řešení po každé úspěšné iteraci. Toto zobrazování je možné vypnout jednoduše přepnutím zobrazení hlavního sešitu na jinou kartu než Fitchart. |
Optimální hodnoty parametrů znázorňuje následující obrázek:
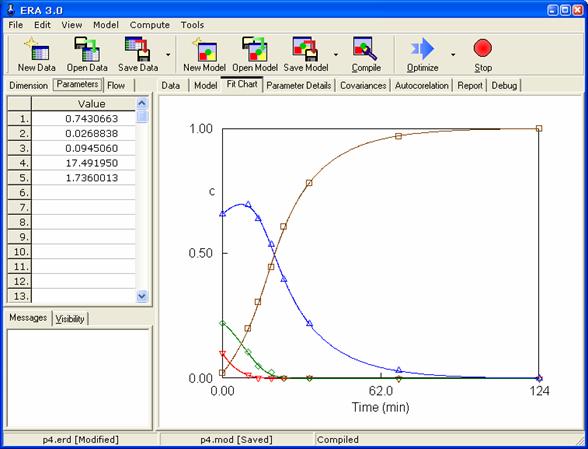
Po ukončení optimalizace je možné přistoupit k výpočtu intervalových odhadů. Výsledky zachycuje další obrázek.
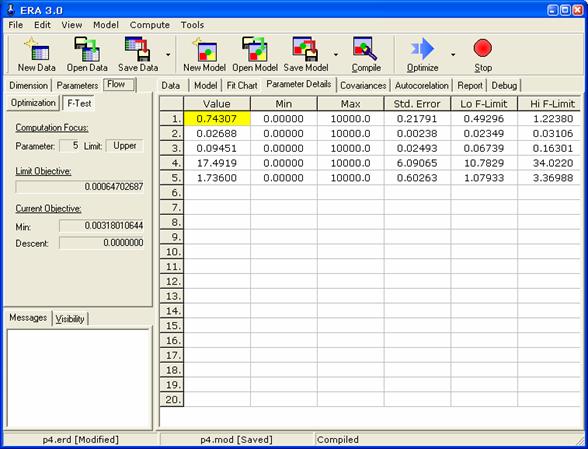
Hodnoty uvedené v matici výsledků na kartě Parameter Details v hlavním sešitě lze tažením myši označit a zkopírovat do schránky Ctrl+C pro další zpracování např. v programu MS Excel.
Je patrné, že konfidenční intervaly jsou výrazně užší než je rozpětí konfidenčních mezí. To je možné vysvětlit vysokými korelacemi (viz kap. 1.3.1) mezi parametry a nesymetrickým tvarem konfidenční oblasti (viz např. obr. 3). V programu ERA 3.0 lze korelační koeficienty vypočítat příkazem Compute/Normalized Covariances. Výsledky se zobrazí na kartě Covariances hlavního sešitu (viz obrázek).
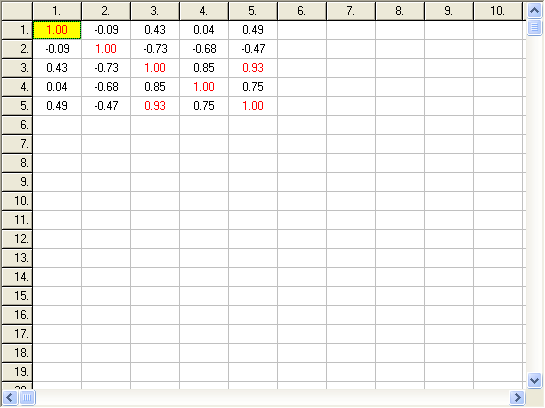
Výsledek:
Porovnání vypočtených intervalových odhadů vede k závěru, že konfidenční intervaly hodnotí parametry jako nerealisticky spolehlivé. Vzhledem k nelinearitě modelu a vysokým korelacím mezi parametry představují konfidenční meze podstatně věrohodnější obraz o spolehlivosti odhadnutých parametrů.
Příklad 5: Významnost parametrů
Zadání:
Ve vsádkovém reaktoru byla sledována následná heterogenně katalyzovaná reakce A ® B ® C. Změřené hodnoty závislosti koncentrace na čase jsou uvedeny v následující tabulce
| t min | 0 | 0.167 | 0.25 | 0.5 | 1 | 2 | 3 | 6.25 | 7 | 7.5 | 9.5 | | cA | 1.000 | 0.949 | 0.927 | 0.905 | 0.780 | 0.638 | 0.409 | 0.214 | 0.178 | 0.157 | 0.088 | | cB | 0.000 | 0.048 | 0.069 | 0.090 | 0.206 | 0.337 | 0.527 | 0.676 | 0.695 | 0.701 | 0.681 | | cC | 0.000 | 0.003 | 0.004 | 0.005 | 0.014 | 0.026 | 0.064 | 0.110 | 0.128 | 0.142 | 0.231 |
| t, min | 12.5 | 15 | 17.5 | 20 | 22.5 | 25 | 27.5 | 30 | 32.5 | 35 | | cA | 0.050 | 0.038 | 0.032 | 0.025 | 0.018 | 0.013 | 0.006 | 0.002 | 0.001 | 0.001 | | cB | 0.599 | 0.432 | 0.304 | 0.239 | 0.158 | 0.090 | 0.047 | 0.018 | 0.008 | 0.002 | | cC | 0.351 | 0.530 | 0.665 | 0.736 | 0.824 | 0.897 | 0.947 | 0.980 | 0.991 | 0.997 |
Jako model použijte soustavu diferenciálních. Rychlostní rovnice použijte v následujícím tvaru:
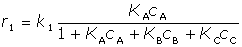 [17-a] [17-a]
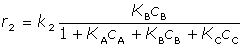 [17-b] [17-b]
Odhadněte optimální hodnoty parametrů, vypočítejte jejich intervalové odhady a korelační koeficienty. Na základě těchto údajů zhodnoťte statistickou významnost parametrů a případně proveďte vyloučení nevýznamných parametrů.
Řešení:
Při řešení příkladu programem ERA je zapotřebí nejprve specifikovat rozměr systému a zadat experimentální data (viz obrázek).
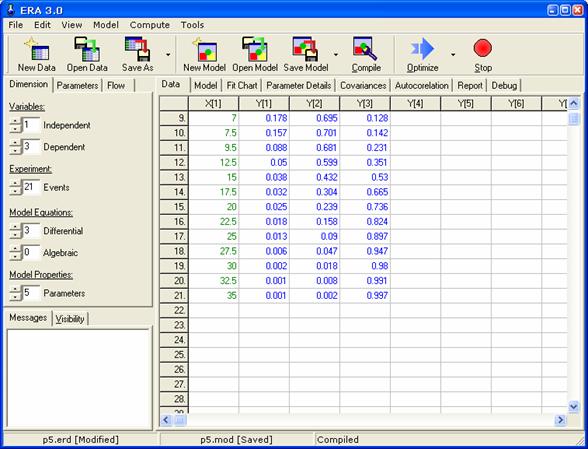
Matematický model bude mít následující tvar:
language=pascal
declar
r1,r2,ads : Double;
end declar
static
end static
dynamic
ads := 1 + p[3]*y[1] + p[4]*y[2] + p[5]*y[3];
r1 := p[1]*p[3]*y[1]/ads;
r2 := p[2]*p[4]*y[2]/ads;
dy[1] := - r1;
dy[2] := r1 - r2;
dy[3] := r2;
end dynamic
Grafické znázornění řešení pro optimální hodnoty parametrů a jejich intervalové odhady jsou znázorněny na následující dvojici obrázků
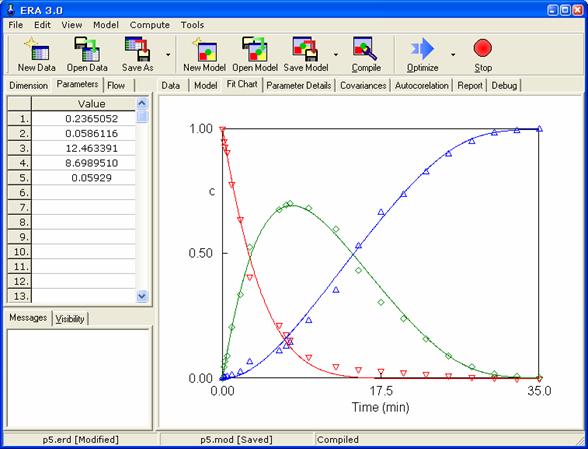
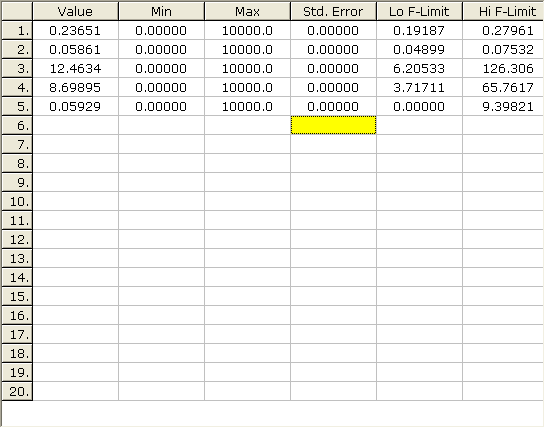
Přestože experimentálních dat je v tomto případě dostatek a jejich rozptyl je poměrně malý, je spolehlivost odhadu některých parametrů velmi nízká. Je to způsobeno vysokými korelacemi parametrů. Navíc je parametr KC statisticky nevýznamný (statisticky nevýznamně odlišný od nuly – viz kap. 1.4) protože rozsah jeho konfidenčních mezí zahrnuje nulu. Nejméně spolehlivé jsou odhady parametrů KA a KB, které jsou nejsilněji korelované s nevýznamným parametrem a také mezi sebou navzájem. Nevýznamnost adsorpčního koeficientu KC je možno interpretovat jako zanedbatelnou sílu sorpce látky C na povrchu katalyzátoru ve srovnání s látkami A a B. Vyloučením parametru KC z adsorpčního členu byl získán zjednodušený model se čtyřmi parametry.
language=pascal
declar
r1,r2,r3,ads : Double;
end declar
static
end static
dynamic
ads := 1 + p[3]*y[1] + p[4]*y[2];
r1 := p[1]*p[3]*y[1]/ads;
r2 := p[2]*p[4]*y[2]/ads;
dy[1] := - r1;
dy[2] := r1 - r2;
dy[3] := r2;
end dynamic
Optimální parametry tohoto zjednodušeného modelu a jejich intervalové odhady ukazuje následující obrázek.
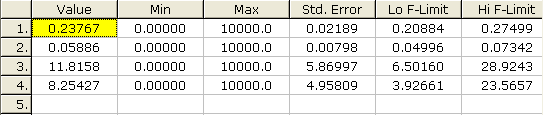
Výsledek:
Vyloučení nevýznamného parametru způsobilo výrazné snížení korelací parametrů. Zjednodušený model byl přitom schopen popsat průběh reakce prakticky stejně dobře jako model původní. Nižší míra korelací parametrů a jejich nižší počet se u zjednodušeného modelu projevuje v poměrně vysoké spolehlivosti odhadnutých parametrů.
| 
