Aplikace techniky ventingu (bioventingu, air-spargingu) v uspořádání in-situ nutně musí předcházet určení hlavních projektových parametrů, kterými jsou:

počet, poloha a rozměry vrtů

odhad časového průběhu sanace.

Určení počtu, polohy a rozměru vrtů

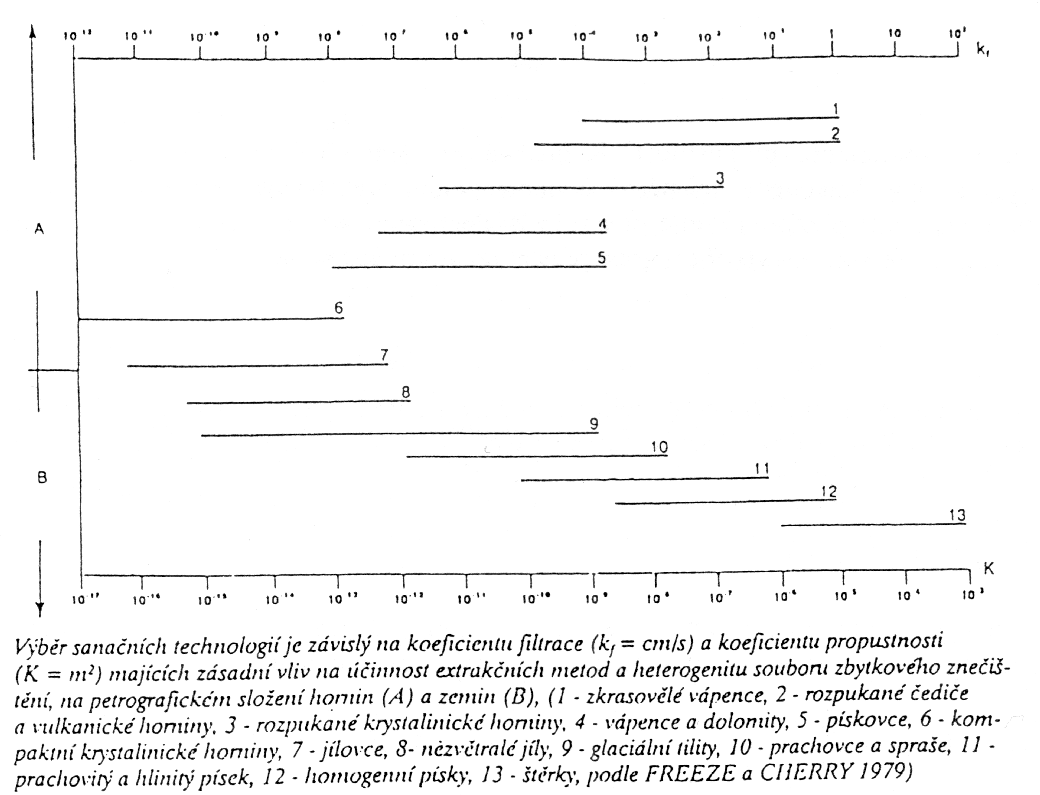
Nejvýznamnějším projektovým parametrem, který musí být zjištěn před zahájením ventingu je schopnost horninového materiálu propouštět vzduch. Materiálovou konstantou vyjadřující míru této schopnosti je koeficient propustnosti K (m²), který je definován v kapitole 5. Hrubý odhad koeficientu propustnosti může být získán z dostupných tabulek nebo diagramů (Obr. 8.1.4), přičemž je ovšem nutné počítat s řádovými chybami. Při odpovědné projektové přípravě je podobný odhad nedostatečný. Dalším způsobem určení propustnosti je finančně nepříliš náročný laboratorní experiment, při kterém se vzorek kontaminované zeminy přenese do laboratorních podmínek a některou z dostupných metodik se koeficient propustnosti určí. Laboratorní posouzení propustnosti přináší ovšem dva základní problémy. Prvním je odběr neporušeného vzorku zeminy - při každém zásahu do kontaminovaného materiálu dochází k narušené jeho struktury, což samozřejmě omezuje věrohodnost tohoto typu stanovení. Druhým problémem je interpretace výsledků na širší okolí odběrového místa. I kdyby byl odběr vzorku proveden bez porušení struktury a laboratorní stanovení bylo bezchybné, je velmi obtížné na základě pouze jediného nebo několika málo experimentálních výsledků posuzovat propustnost většího prostoru kontaminované zeminy. V praxi lze laboratorní měření použít pouze u homogenních materiálů. Třetím a nejčastěji používaným způsobem je poloprovozní určení koeficientu propustnosti, při kterém mohou být současně zjištěny i další projektové parametry. Metodika poloprovozní ventingové zkoušky (tzv. Johnsonův test) je vysvětlena dále.

 

Obr. 8.1.4: Hrubý odhad propustnosti horninového materiálu na základě obecné klasifikace

Na lokalitě, která je uvažována pro aplikaci ventingu, je vyhlouben zkušební odsávácí vrt a v určitých vzdálenostech od jeho středu potom řada vrtů monitorovacích (přinejmenším tři vrty). Pod pojmem monitorovací vrt je zde chápán maloprůměrový vrt, který je určen pro měření aktuálního dosahovaného podtlaku. Odsávací vrt je opatřen kompresorem a je zahájeno odčerpávání vzduchu, při kterém je udržována konstantní průtoková rychlost. V průběhu poloprovozního ověření je potom v monitorovacích vrtech sledován aktuální dosažený podtlak, který je posléze vynášen jako funkce času.

Lze odvodit, že při konstantní průtokové rychlosti odsávaného vzduchu Q se aktuální dosahovaný podtlak P mění v čase podle rovnice:

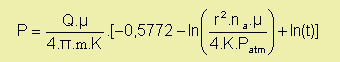
kde  m (cm) - průměr odsávacího vrtu
            µ (g . cm^-1. s^-1 ) - dynamická viskozita vzduchu
            r (cm) - vzdálenost mezi odsávacím vrtem a monitorovacím vrtem
            P_atm (g . cm^-1. s^-2) - absolutní atmosférický tlak
            n_a (%) - podíl pórů vyplněných vzduchem
            Q (cm³. s^-1) - průtoková rychlost vzduchu

Jednotkou propustnosti K ve výše uvedeném vztahu je Darcy (1 Darcy = 10^-8 cm²). Vyneseme-li časovou závislost dosahovaných podtlaků pro každý monitorovací vrt a proložíme-li tuto závislost lineární regresí, potom sklon S (g . cm^-1 . s^-2) takto získané přímky je úměrný koeficientu propustnosti K podle vztahu:

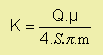
Hodnoty koeficientu propustnosti K zjištěné pro jednotlivé monitorovací vrty jsou poté zprůměrovány a takto stanovená průměrná hodnota potom představuje parametr platný pro okolí daného vrtu. Pokud dále předpokládáme lineární závislost mezi aktuálním dosahovaným podtlakem P a hodnotami log (r), je možné vytvořit regresi přes n monitorovacích vrtů:

Aproximací na nulovou hodnotu podtlaku můžeme potom zjistit vzdálenosti R, při které se již vliv odsávání vzduchu neprojeví. Tato vzdálenost tedy odpovídá dosahu vrtu, kterou můžeme zjistit z rovnice:

        (při Q = konst.)

Konečně pokud předpokládáme lineární závislost mezi dosahem vrtu R a průtokovou rychlostí Q, můžeme zjistit dosah vrtu pro libovolnou zvolenou průtokovou rychlost:

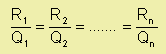
Minimální počet vrtů (N_min) potřebný pro sanaci kontaminovaného území o ploše A (m²) můžeme vypočítat z rovnice:

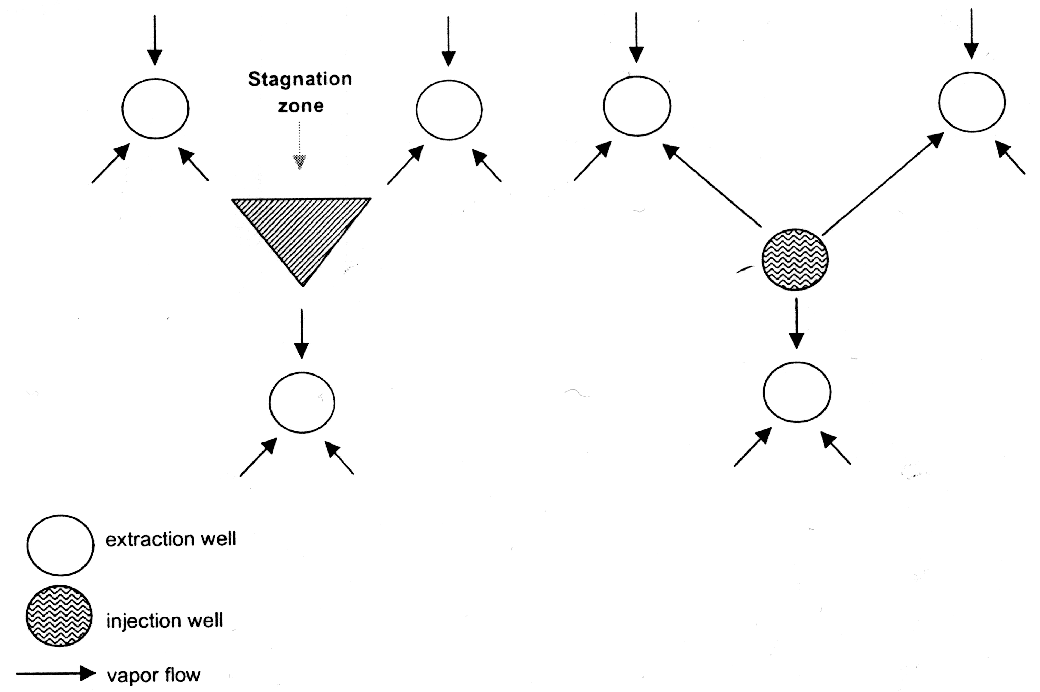
V souvislosti s potřebným počtem vrtů je nutné upozornit rovněž na význam rozmístění vrtů. Na Obr. 8.1.5. je ukázáno trojúhelníkové (geometricky nejúčinnější) rozmístění odsávacích vrtů. V důsledku kruhového dosahu vrtů může vznikat mezi těmito vrty tzv. stagnační zóna, ve které nedochází k pohybu vzduchu. Možným opatřením je v tomto případě instalace jednoho vrtu vtlačovacího, který zajistí transport i v tomto hluchém prostoru. Myšlenka vzniku stagnační zóny je ovšem značně idealizované a platí tím méně, čím více je sanované prostředí heterogenní.

Obr. 8.1.5.: Vliv vtlačovacího vrtu na účinnost sanace ventingem

Odhad časového průběhu sanace

Vedle počtu a rozmístění vrtů je další zásadní podmínkou správné aplikace techniky ventingu znalost časového průběhu sanace. Na základě prognózy časového průběhu je možné stanovit dobu ukončení sanace (pro daný sanační limit) a dále je možné odhadnout některé parametry zařízení, na kterém je odsávaný vzduch následně čištěn (například velikost adsorpční jednotky.

V současné době existuje řada matematických modelů a výpočetních programů (většina z nich je dostupná komerčně) použitelných s větší či menší přesností pro simulaci transportních procesů probíhajících při aplikaci ventování. U jednoduchých modelů opírajících se o několik málo vstupních parametrů je ovšem nutná zvýšená opatrnost při interpretaci výsledků. Složitější modely se potom vyznačují značnou matematickou náročností, nutností znalosti velkého množství vstupních parametrů (z nichž řada je obtížně měřitelná) a nutností multioborového přístupu (kombinace poznatků hydrogeologie, chemie a dalších oborů).

Pro hrubý odhad použitelnosti technologie ventingu (nebo pro její případné vyloučení tam, kde z objektivních důvodů metodu použít nelze) je ovšem možné použít modelů idealizovaných, u kterých je na úkor přesnosti výrazně snížena matematická náročnost a počet vstupních parametrů. Postup odvození jednoho z možných idealizovaných modelů byl ukázán výše v kapitole 6. Pro připomenutí tedy uvádíme předpoklady, ze kterých tento model vychází:

 kontaminovaná zemina je v celém objemu homogenní (charakteristiky této zeminy se v rámci kontaminovaného objemu významně nemění

 transportní procesy probíhající při průchodu vzduchu zeminou (např. přechod trichlorethylenu z pevné fáze do vzduchu) jsou natolik pomalé, že se stav v zemině blíží stavu rovnovážnému

 v průběhu sanace se významně nemění vlastnosti zeminy

 v rámci probíhajících dějů nebude trichlorethylen odstraňován jinými procesy (například biodegradačními pochody).

Všechny čtyři výše uvedené předpoklady jsou silně idealizující a jejich přijetí v rámci jakéhokoli sanačního procesu by jistě bylo značně diskutabilní. Akceptujeme-li ovšem tyto podmínky, můžeme výrazně zjednodušit potřebný matematický aparátu a výsledek, ke kterému na základě takto přijatých předpokladů dojdeme, je potom výsledkem ideálním, a tedy za daných podmínek nejlepším možným. Tato skutečnost začíná být důležitá v okamžiku, kdy i takto idealizovaný model vykáže neúměrně dlouhou dobu potřebnou pro ukončení sanace.