1.6.7 Výpočet Henryho konstanty
Při 25 °C se při parciálním tlaku chloru 0,1 MPa v 1 dm3 ethylbenzenu rozpustí 1,66 mol Cl2. Určete (a) Henryho konstantu Cl2 a (b) jeho rozpustnost v ethylbenzenu (v gramech chloru na litr čistého ethylbenzenu) při téže teplotě za parciálního tlaku chloru 0,037 MPa. Hustota ethylbenzenu je 0,8626g cm−3, Methylbenzen = 106,17 g mol−1, MCl = 35,5 g mol−1. Předpokládejte platnost Henryho zákona ve tvaru p2 = x2KH.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
(a) KH = 589,45 kPa (x2 = 0,16965)
(b) n = 0,54414 mol dm−3, rozpustnost = 38,634 g dm−3 (x2 = 6,277 . 10−2)
Postup
Z dat určíme Henryho konstantu a pak zpětně vypočteme látkové množství rozpuštěného plynu za nižšího tlaku. Nakonec převedeme na hmotnost na litr ethylbenzenu.
Audio
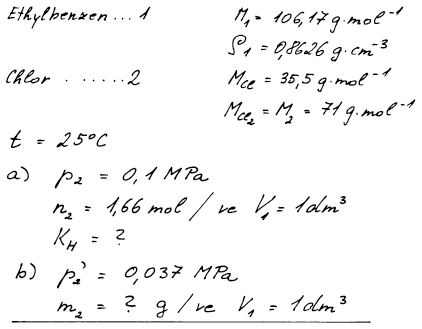
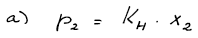
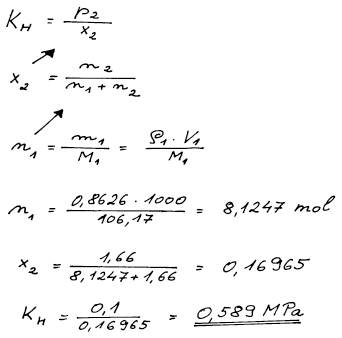
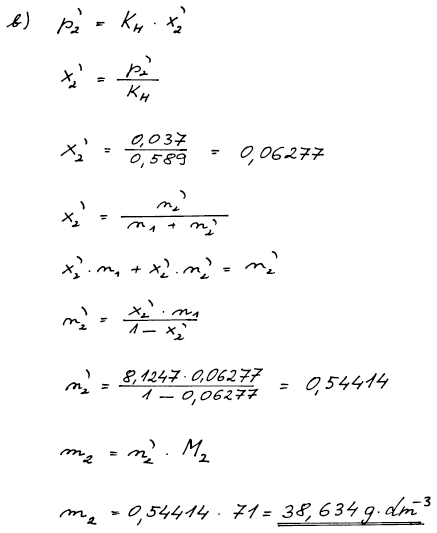
Binární systém. Chlor je nad svou kritickou teplotou, a proto se jedná
o rovnováhu kapalina–plyn nebo také o rozpustnost
plynů. Rozpustností se rozumí rovnovážná koncentrace plynu
v rozpouštědle za dané teploty a tlaku.
Za předpokladu ideálního chování plynné fáze rovnováhu popisuje
Henryho zákon, kde konstanta lineární závislosti parciálního tlaku
plynu nad roztokem na molárním zlomku rozpuštěného plynu se nazývá
Henryho konstantou.
K výpočtu Henryho konstanty z Henryho zákona potřebujeme vedle
parciálního tlaku chloru nad roztokem ještě rovnovážný molární zlomek
chloru v ethylbenzenu.
Z Henryho zákona vypočteme molární zlomek chloru v rovnováze. Teplota
je konstantní a tak můžeme využít Henryho konstantu, kterou jsme
vypočetli v první části příkladu. Dále známe parciální tlak chloru nad
roztokem.