10.4.1 Výpočet teploty varu při přehánění vodní parou
Vodu(1) a nitrobenzen(2) lze považovat za prakticky nemísitelné kapaliny. Určete teplotu, při které bude heterogenní směs nitrobenzenu a vody destilovat za tlaku 100 kPa. Určete dále složení parní fáze a hmotnost nitrobenzenu, který oddestiluje se 100 g vody. Výparná entalpie vody při normálním bodu varu je 40,64 kJ.mol−1, tlak nasycených par nitrobenzenu při 100 °C je 3 kPa a při 150 °C 19,8 kPa.
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
(T = 371,98 K = 98,83 °C), m2 = 20,1 g
Řešení
Tlak par nad dvěma nemísitelnými kapalinami je určen rovnicí
![]()
Tuto rovnici pro neznámou T můžeme řešit zkusmo nebo např. Newtonovou metodou. Protože známe při teplotě 100 °C tlaky nasycených par obou látek a výsledná teplota nebude od teploty 100 °C příliš odlišná, je výhodné použít Newtonovu metodu. Jako první aproximaci použijeme 100 °C. Potom můžeme psát (To = 373,15 K)
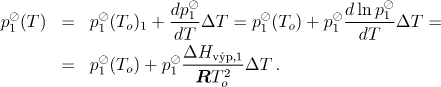
Analogickou rovnici napíšeme pro druhou látku a po spojení s rovn. (10.40) získáme vztah
![]()
z nějž je možno určit ΔT.
Pro výpočet potřebujeme znát ještě hodnotu ΔHvýp nitrobenzenu, kterou určíme ze vztahu:
![]()
Dosazením tohoto výsledku do rovn. (10.41) dostaneme
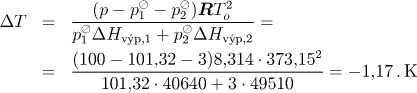
Další aproximací teploty je hodnota 100−1,17 = 98,83 °C. Tlaky nasycených par při této teplotě určíme z integrované Clausiovy–Clapeyronovy rovnice
![]()
a při teplotě 98,83 °C získáme hodnoty ![]() = 97,24 kPa a
= 97,24 kPa a ![]() = 2,85
kPa. Jejich součet s dostatečnou přesností poskytuje hodnotu 100
kPa a není nutno již provádět další krok v Newtonově metodě.
Složení parní fáze je dáno vztahem
= 2,85
kPa. Jejich součet s dostatečnou přesností poskytuje hodnotu 100
kPa a není nutno již provádět další krok v Newtonově metodě.
Složení parní fáze je dáno vztahem
![]()
Hmotnost nitrobenzenu, který oddestiluje se 100 g vody, určíme z molárního zlomku y2:
![]()
kde m1 = 100 g a M1 resp. M2 jsou molární hmotnosti složek. Ze vztahu (10.43) odvodíme
![]()
![[Maple Math]](images/fazXVIII2.gif)
![[Maple Math]](images/fazXVIII3.gif)
![[Maple Math]](images/fazXVIII7.gif)