6.2.3 Výpočet pH roztoků silných a slabých kyselin a zásad
Vypočítejte hodnoty pH následujících vodných roztoků o
koncentracích 0,1 a 0,01 mol/dm3 při teplotě 25 °C:
a) jednosytné kyseliny HA, která se ve vodném roztoku chová jako
silný elektrolyt, tzn. je zcela disociována,
b) slabých jednosytných kyselin HA s disociačními konstantami
KHA = 10−1, 10−2, 10−3, 10−4, 10−5 a 10−6,
c) silné zásady typu BOH,
d) slabých zásad BOH s disociačními konstantami KBOH = 10−1, 10−2, 10−3, 10−4, 10−5 a 10−6.
Iontový součin vody má při teplotě 25 °C hodnotu Kv = 1 . 10−14. Standardní stav: Ideální roztok o
koncentraci c° = 1 mol/dm3. Předpokládejte jednak
ideální chování
, jednak platnost limitního Debyova-Hückelova
vztahu (A = 1,1762( dm3/ mol)1/2).
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
Výsledek
Viz tabulky v Řešení tohoto příkladu.
Řešení
a) Silná kyselina je ve vodném roztoku zcela disociována,
proto platí cH3O+ = cpoč(HA). Za předpokladu ideálního chování roztoků je možno nahradit aktivity koncentracemi a z definičního vztahu pro pH vypočítat hodnoty
V případě neideálního chování budeme vycházet z limitního Debyeova-Hückelova vztahu (pro jednoduchost používáme tohoto vztahu i při koncentracích větších než 0,01), kdy pro aktivitní koeficient hydroxoniového iontu (u plně disociovaného uni-uni valentního elektrolytu I = cpoč) platí
V daném případě tak pro cpoč = 0,1 mol/ dm3 získáme hodnoty aktivitního koeficientu kationtu γ+ = 0,6894 a v případě cpoč = 0,01 mol/ dm3 je γ+ = 0,8890. Odpovídající pH jsou
b) Slabá kyselina ve vodném roztoku částečně disociuje
podle rovnice
Použijeme-li k vyjádření koncentrace iontů a nedisociované kyseliny v roztoku stupeň disociace α, definovaný výrazem
pak z bilance vychází, že
Pokud uvažujeme ideální chování a nepříliš koncentrované roztoky, je možno aktivitu vody považovat za jednotkovou a aktivity iontů a nedisociované kyseliny aproximovat koncentracemi. Pro disociační konstantu slabé kyseliny potom platí
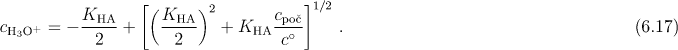
U slabých kyselin s relativně malým stupněm disociace lze
pro 
v rovnici (6.16)
zanedbat koncentraci disociovaného podílu proti původní
koncentraci, takže 
a pro
disociační konstantu lze pak psát
Hodnoty pH, získané na základě vztahu (6.17) (označeny hvězdičkou) i přibližným výpočtem podle (6.18) jsou shrnuty v tab. 6.1 pro koncentrace 0,1 a 0,01 mol/dm3. Výpočet byl proveden u kyselin s disociačními konstantami od 10−1 do 10−6.
Přihlédneme-li k neideálnímu chování, získáme i v případě jednoduchého limitního Debyeova-Hückelova zákona mnohem komplikovanější vztahy. Nadále budeme uvažovat jednotkovou aktivitu vody a jednotkové aktivitní koeficienty neelektrolytů (tj. i jednotkové aktivitní koeficienty HA, BOH ap.). Výraz pro disociační konstantu slabé kyseliny potom můžeme psát ve tvaru
Vyjádříme-li aktivitní koeficient ze vztahu (6.14), dostaneme (I = αcpoč ) relaci
Řešení tohoto vztahu je popsáno ve skriptech Fyzikální chemie I v oddíle 6.8.1. Aktivita vodíkových iontů resp. pH je dáno výrazem
Určené hodnoty α a pH jsou shrnuty v tab.6.1 (vždy poslední dva sloupce).
c) Silná zásada ve vodném roztoku rovněž zcela disociuje podle rovnice
Ze stechiometrie plyne, že cOH− = cB+ = cpoč. Koncentraci hydroxoniových iontů vyjádříme pomocí iontového součinu vody (Kv = aH+aOH− )
a pak vychází
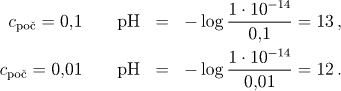
Pro neideální
chování aproximované Debyeovým-Hückelovým limitním vztahem
dostaneme stejně jako v případě ad a) hodnoty 
pro koncentraci c = 0,1 mol/dm3 a
γOH− = 0,8890 pro c = 0,01 mol/dm3. Po dosazení
těchto hodnot do rovnice
dostaneme hodnoty pH = 12,838 a pH = 11,949.
d) Z bilance koncentrací složek při disociaci slabé
jednosytné zásady podle rovnice (6.19)
vychází
Za předpokladu ideálního chování lze pro disociační konstantu zásady odvodit vztah
Pro případ, že platí 
, je opět možno ve jmenovateli zanedbat disociovaný podíl
proti analytické koncentraci zásady a 
.
Tak dostaneme jednoduchý vztah
Odpovídající koncentraci hydroxoniových iontů vyjádříme pomocí iontového součinu vody
Obecné řešení rovnice (6.20) představuje vztah
Hodnoty pH, získané přibližným i přesným (označeno hvězdičkou) výpočtem (za předpokladu ideálního chování), uvádí pro obě zvolené koncentrace tab.6.2.
Uvažujeme-li reálné chování, pak (za podobných aproximací jako v předcházejích případech) dostaneme pro disociační konstantu zásady KBOH relaci
(platící pro uni-uni valentní zásadu). Z této rovnice určíme neznámý disociační stupeň α odpovídající konkrétnímu zadání (viz oddíl 6.8.1 ve skriptech FCH I). Pro pH lze odvodit vztah
Hodnoty α a pH vypočtené na základě rovnic (6.22) a (6.23) jsou uvedeny v tab.6.2 (vždy poslední dva sloupce).