1. Definice (včetně zjednodušení) popisovaného systému
Představme si vrt vyhloubený na lokalitě kontaminované trichlorethylenem. Předpokládejme:
1) že horninový materiál v okolí vrtu je homogenní (tj. jeho zrnitost, porozita, charakter kontaminace, a další parametry se nemění). Na tento vrt instalujeme kompresor (jedná-li se o kontaminaci nesaturované zóny a sanace spočívá v odsávání znečištěného vzduchu) nebo čerpadlo (jedná-li o kontaminaci saturované zóny a sanace spočívá v odčerpávání znečištěné podzemní vody. Vrt je dokonale utěsněn, přičemž jeho hloubka je známa (rovněž známe úroveň hladiny podzemní vody a úroveň nepropustného podloží). Předpokládejme dále:
2) že na sanaci se nebude podílet více nežli jedna sanační technika (tedy pouze odsávání vzduchu při čištění nesaturované zóny nebo pouze sanační čerpání při čištění saturované zóny) a:
3) že popisovaný systém - zemina kontaminovaná trichlorethylenem - je v každém okamžiku v rovnováze.
Dále budeme předpokládat:
4) že tlakový gradient vytvořený kompresorem nebo čerpadlem bude soustředně rozložen okolo vyhloubeného vrtu.
2. Sestavení bilanční rovnice
Výše definovaný a zjednodušený systém - tedy vrt vyhloubený do určité hloubky v lokalitě kontaminované trichlorethylenem a opatřený kompresorem nebo čerpadlem - může být následně popsán řadou více či méně složitých matematických vztahů. Provádí-li sestavení bilanční rovnice (nebo rovnic) chemický inženýr, přirozeně vykazuje snahu opřít se o popis jemu známých inženýrských poznatků a snaží se nalézt podobnost mezi definovaným systémem a běžnými chemicko-inženýrskými technologickými soustavami. Jednou z možností, která se nabízí je například paralela mezi naší kontaminovanou zeminou a kolonou vyplněnou porézním materiálem, kterou protéká vzduch nebo voda a v níž dochází k přenosu hmoty mezi jednotlivými fázemi. Můžeme si tedy představit, že tato kolona je vyplněna zrnitým sorpčním materiálem obsahujícím určité množství trichlorethylenu, přičemž do kolony přichází čistý vzduch nebo čistá voda, která se při průchodu kolonou nasytí trichlorethylenem a odchází z kolony. Výše přijatá podmínka předpokládající v každém okamžiku rovnovážný stav potom značí, že nasycení odcházejícího vzduchu nebo vody potom odpovídá rovnovážnému (teoreticky maximálnímu) nasycení.
Odčerpáme-li tedy na výstupu z kolony (nebo na výstupu z vrtu) infinitezimální (blížící se nekonečně malému) objem vzduchu dV, potom množství (například molární) trichlorethylenu odtaženého s tímto vzduchem bude:
![]()
kde C představuje rovnovážnou koncentraci trichlorethylenu v odcházejícím vzduchu.
Tuto jednoduchou diferenciální rovnici lze při definování počátečních a koncových podmínek řešit buď analyticky nebo numericky. Je-li tedy naší hypotetickou kolonou nebo kontaminovanou zeminou prosáván vzduch, lze analytickým řešením dojít ke vztahu:
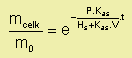
kde mcelk - celková zbývající hmotnost trichlorethylenu v zemině
mo - celková počáteční hmotnost trichlorethylenu v zemině
P - průtoková rychlost vzduchu
Kas - rozdělovací koeficient vzduch/zemina
Hs - hmotnost zeminy
V - objem vzduchu v pórech zeminy
t - čas
V případě odčerpávání znečištěné podzemní vody lze analytickým řešením výše uvedené diferenciální rovnice dojít k řešení:
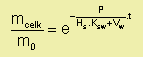
kde mcelk - celková zbývající hmotnost trichlorethylenu v zemině
mo - celková počáteční hmotnost trichlorethylenu v zemině
P - průtoková rychlost vody
Ksw - rozdělovací koeficient zemina/voda
Hs - hmotnost zeminy
Vw - objem vody v pórech zeminy
t - čas
S pomocí výše uvedených rovnic, případně s pomocí numerických postupů, lze tedy provést kvantifikaci potřebných technických parametrů. Známe-li například základní technické parametry čerpadla nebo kompresoru a koeficient propustnosti dané zeminy, je možné vypočítat průtokovou rychlost. Známe-li průtokovou rychlost (množství vzduchu nebo vody odčerpávané z vrtu) je možné s pomocí výše uvedených rovnic určit čas potřebný na dosažení požadované zbytkové úrovně znečištění. Koncovým výstupem takovéhoto výpočtu je tedy závislost zbytkového množství kontaminující látky na čase. Tato závislost (a» už zjištěná jakkoli) může potom být účelným rozhodovacím podkladem při vypracování sanačního projektu.
Pokud bychom provedli výpočet naznačený v předchozím odstavci a srovnali takto vypočítanou časovou závislost zbytkové kontaminace se skutečným časovým úbytkem kontaminace téměř jistě bychom zjistili, že vypočítaná a reálná závislost se významně odlišují (reálný pokles kontaminace bude pravděpodobně výrazně pomalejší). Chceme-li náš model dále zpřesňovat, bez toho abychom se pouštěli do podrobnějšího zkoumání probíhajících mechanismů, můžeme nyní učinit krok, který z daného modelu vlastně teprve činí model semiempirický - totiž s pomocí jedné nebo více neexaktně zjištěných číselných konstant upravit náš model tak, aby dostatečně přesně vystihoval skutečné chování námi popisovaného systému.
Vztah mezi výchozími podmínkami a přesností modelu
Podíváme-li se nyní blíže na jednotlivé podmínky, z nichž náš semiempirický model vychází, můžeme nalézt některé z možných příčin rozdílu mezi vypočítanou a skutečnou časovou závislostí úbytku kontaminace. Podmínky, o které se tento model opíral byly následující:
1. horninový materiál v okolí vrtu je homogenní
2. na sanaci se nebude podílet více nežli jedna sanační metoda
3. popisovaný systém - zemina kontaminovaná trichlorethylenem - je v každém okamžiku v rovnováze
4. tlakový gradient vytvořený kompresorem nebo čerpadlem bude soustředně rozložen okolo vyhloubeného vrtu