>
restart;
Neprve provedeme výpočet pro ideální plyn
>
R:=8.314;
![[Maple Math]](images/staXIV1.gif)
>
T:=325+273.15;
![[Maple Math]](images/staXIV2.gif)
>
Vm:=0.34*10^(-3);
![[Maple Math]](images/staXIV3.gif)
>
p:=R*T/Vm;
![[Maple Math]](images/staXIV4.gif)
Dále použijeme van der Waalsovu stavovou rovnici
>
restart;
>
p:=R*T/(Vm-b)-a/Vm^2;
![[Maple Math]](images/staXIV5.gif)
Pro určení konstant nejprve vypočteme první dvě derivace tlaku podle objemu
>
d1:=diff(p,Vm);
![[Maple Math]](images/staXIV6.gif)
>
d2:=diff(d1,Vm);
![[Maple Math]](images/staXIV7.gif)
V kritickém bodě platí následující tři rovnice: 1. a 2. derivace jsou nulové a tlak je roven kritickému tlaku
>
r1:=subs(Vm=Vc,T=Tc,d1=0);
![[Maple Math]](images/staXIV8.gif)
>
r2:=subs(Vm=Vc,T=Tc,d2=0);
![[Maple Math]](images/staXIV9.gif)
>
r3:=subs(Vm=Vc,T=Tc,p=pc);
![[Maple Math]](images/staXIV10.gif)
Konstanty stavové rovnice a kritický objem dostaneme řešením soustavy předchozích tří rovnic
>
reseni:=solve({r1,r2,r3},{a,b,Vc});
![[Maple Math]](images/staXIV11.gif)
a provedeme tedy jejich dosazení
>
assign(reseni);
Nyní již mužeme z kritických veličin konstanty vypočítat
>
R:=8.314;
![[Maple Math]](images/staXIV12.gif)
>
Tc:=405.5;
![[Maple Math]](images/staXIV13.gif)
>
pc:=11.35*10^6;
![[Maple Math]](images/staXIV14.gif)
>
evalf(a);
![[Maple Math]](images/staXIV15.gif)
>
evalf(b);
![[Maple Math]](images/staXIV16.gif)
Dosazením molárního objemu a teploty pak získáme požadovaný tlak
>
T:=325+273.15;
![[Maple Math]](images/staXIV17.gif)
>
Vm:=0.34*10^(-3);
![[Maple Math]](images/staXIV18.gif)
>
p;
![[Maple Math]](images/staXIV19.gif)
Analogicky můžeme postupovat pro Redlichovu-Kwongovu rovnici
>
restart;
>
p:=R*T/(Vm-b)-a/(sqrt(T)*Vm*(Vm+b));
![[Maple Math]](images/staXIV20.gif)
Pro určení konstant opět vypočteme první dvě derivace tlaku podle objemu
>
d1:=diff(p,Vm);
![[Maple Math]](images/staXIV21.gif)
>
d2:=diff(d1,Vm);
![[Maple Math]](images/staXIV22.gif)
V kritickém bodě platí následující tři rovnice: 1. a 2. derivace jsou nulové a tlak je roven kritickému tlaku
>
r1:=subs(Vm=Vc,T=Tc,d1=0);
![[Maple Math]](images/staXIV23.gif)
>
r2:=subs(Vm=Vc,T=Tc,d2=0);
![[Maple Math]](images/staXIV24.gif)
>
r3:=subs(Vm=Vc,T=Tc,p=pc);
![[Maple Math]](images/staXIV25.gif)
Nyní se pokusíme nalézt řešení
>
reseni:=solve({r1,r2,r3},{a,b,Vc});
![[Maple Math]](images/staXIV26.gif)
![[Maple Math]](images/staXIV27.gif)
Je vidět, že tentokrát soustava vede ke kubické rovnici, která má obecně tři řešení.
>
allvalues(reseni);
![[Maple Math]](images/staXIV28.gif)
![[Maple Math]](images/staXIV29.gif)
![[Maple Math]](images/staXIV30.gif)
Pouze první řešení je fyzikálně opodstatněné (neobsahuje komplexní čísla). Provedeme tedy jeho dosazení
>
assign(%[1]);
a vyčíslime vyjádření konstant pomocí kritických veličin
>
evalf(a);
![[Maple Math]](images/staXIV31.gif)
>
evalf(b);
![[Maple Math]](images/staXIV32.gif)
Na závěr opět určíme jejich hodnoty
>
R:=8.314;
![[Maple Math]](images/staXIV33.gif)
>
Tc:=405.5;
![[Maple Math]](images/staXIV34.gif)
>
pc:=11.35*10^6;
![[Maple Math]](images/staXIV35.gif)
>
evalf(a);
![[Maple Math]](images/staXIV36.gif)
>
evalf(b);
![[Maple Math]](images/staXIV37.gif)
a osazením molárního objemu a teploty získáme požadovaný tlak
>
T:=325+273.15;
![[Maple Math]](images/staXIV38.gif)
>
Vm:=0.34*10^(-3);
![[Maple Math]](images/staXIV39.gif)
>
evalf(p);
![[Maple Math]](images/staXIV40.gif)
>
![]()
![]()
![]()
![]()
![]()
![]()
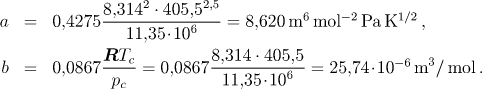
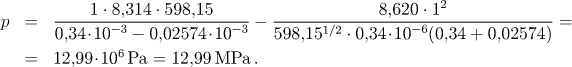
![[Maple Math]](images/staXIV5.gif)
![[Maple Math]](images/staXIV6.gif)
![[Maple Math]](images/staXIV7.gif)
![[Maple Math]](images/staXIV8.gif)
![[Maple Math]](images/staXIV9.gif)
![[Maple Math]](images/staXIV10.gif)
![[Maple Math]](images/staXIV11.gif)
![[Maple Math]](images/staXIV21.gif)
![[Maple Math]](images/staXIV22.gif)
![[Maple Math]](images/staXIV23.gif)
![[Maple Math]](images/staXIV24.gif)
![[Maple Math]](images/staXIV26.gif)
![[Maple Math]](images/staXIV27.gif)
![[Maple Math]](images/staXIV28.gif)
![[Maple Math]](images/staXIV29.gif)
![[Maple Math]](images/staXIV30.gif)
![[Maple Math]](images/staXIV31.gif)