2.1 Reálné plyny a kapaliny
Pro popis stavového chování plynů za vyšších tlaků a kapalin nevystačíme s stavovou rovnicí ideálního plynu, ale používáme složitějších rovnic.
V oblasti nepříliš vysokých tlaků je pro plyn možno použít objemový viriální rozvoj, ve kterém je kompresibilitní faktor vyjádřen ve tvaru řady v mocninách 1/Vm, respektive v mocninách c
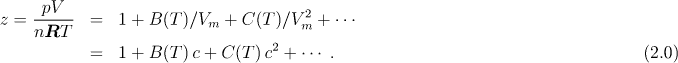
Veličiny B,C,… se nazývají viriální koeficienty; B je druhý viriální koeficient, C třetí viriální koeficient, atd.
Podobně je definován tlakový viriální rozvoj, ve kterém je kompresibilitní faktor vyjádřen ve tvaru řady v mocninách p
![]()
Pro popis stlačených plynů a kapalin se používá van der Waalsova stavová rovnice
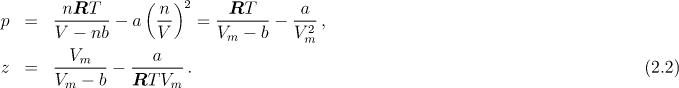
kde a a b jsou konstanty stavové rovnice, nebo přesnější Redlichova-Kwongova stavová rovnice
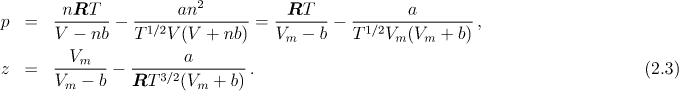
Závislost molárního objemu nasycené kapaliny na teplotě popisuje Rackettova stavová rovnice
![]()
kde zc je kompresibilitní faktor v kritickém bodě.
Pro popis závislosti objemu kapalin na teplotě se v užším rozmezí teplot používá koeficient izobarické roztažnosti αp.
![]()
Pro závislost na tlaku pak koeficient izotermické stlačitelnosti κT.
![]()
Příklady:
2.1.1 Výpočet objemu z tlakového virálního rozvoje (2.1.2 Určení druhého viriálního koeficientu (
2.1.3 Výpočet objemu z objemového viriálního rozvoje (
2.1.4 Vyjádření izotermní kompresibility z tlakového viriálního rozvoje (
2.1.5 Viriální koeficient z van der Waalsovy rovnice (
2.1.6 Odhad druhého viriálního koeficientu (
2.1.7 Výpočet tlaku plynu ze stavových rovnic (
2.1.8 * Výpočet kritického kompresibilitního faktoru (
2.1.9 Výpočet tlaku z van der Waalsovy rovnice (
2.1.10 Výpočet tlaku ze stavových rovnic (
2.1.11 * Výpočet množství látky z van der Waalsovy rovnice (
2.1.12 Aplikace koeficientu roztažnosti a stlačitelnosti (
2.1.13 Závislost objemu kapalin na tlaku (
2.1.14 Závislost objemu kapalin na teplotě (
2.1.15 Odhad teplotní závislost hustoty nasycené kapaliny (