| # | Název | Zadání | OS |
|---|
| 000 | Vlastní téma | Máte-li něco zajímavého, kontaktujte vhodného vyučujícího! | |
| q01 | Vlastnosti benzynu | Benzyn je důležitým reaktivním meziproduktem v některých organických reakcích. V protokolu z této úlohy popište jeho základní vlastnosti a význam a metodami počítačové chemie vypočítejte strukturu benzynu, hydrogenační entalpii a Gibbsovu energii v plynné fázi při teplotě 300 K a vibrační frekvence. Vibrační frekvence přiřaďte jednotlivým pohybům. | 2G |
| q02 | Sloučeniny vzácných plynů | Vypočítejte vlastnosti molekuly KrF2 a její isoelektronické struktury KrO22−. | 4G |
| q03 | Pravá a nepravá vodíková vazba | Vypočítejte strukturu, vibrační frekvence a vazebnou energii dimeru flurovodíku a dimeru difluormethanu. Jak se mění frekvence X-H vazeb v komplexu v porovnání s monomerem? Jak se mění geometrie monomeru v komplexu? Porovnejte vazebné energie vodíkové vazby s typickou vazebnou energií kovalentní vazby. Do protokolu přidejte kratší pojednání o významu van der Waalsovských interakcí v přírodních vědách. Literatura: Chem. Listy 102 (2008) 884. | 3G |
| q04 | Klastry vody | Vypočítejte strukturu a interakční energii pro dimer, trimer a tetramer vody. Srovnejte bázi 6-31g* s bází 6-31+g*, která obsahuje difúzní funkce. Vypočítejte rovnovážnou konstantu dimerizace vody. Do protokolu přidejte kratší pojednání o významu van der Waalsovských interakcí v přírodních vědách. Literatura: Proc. Natl. Acad. Sci. 98 (2001) 10533, The Cambridge Energy Landscape Database. | 3G |
| q05 | Izomerace glyoxalu | Vypočítejte strukturu a energie cis a trans glyoxalu. Vypočítejte aktivační energii pro izomeraci, případně také reakční profil. Jaká je rovnovážná konstanta izomerace? Dokázali byste odhadnout rychlostní konstantu izomerace na základě teorie transitního stavu? V úvodu stručně popište teoretické metody výpočtu rychlostních konstant. | 4G |
| q06 | Dimer helia | Studujte vliv velikosti báze a stupeň zahrnutí korelačních efektů na vazebnou energii dimeru helia. Studujte báze cc-pVDZ, aug-cc-pVDZ, aug-cc-pVTZ, aug-cc-pVQZ a metody HF, MP2 a CCSD(T). Porovnejte interakční energii s typickou hodnotou termální energie. V úvodu diskutujte význam disperzní energie v chemii a biologii. | 2G |
| q07 | Ab initio studium SN2 reakce | Vypočítejte energii reaktantů, produktů a tranzitního stavu pro modelovou reakci fluoridového aniontu s methylfluoridem mechanismem SN2. Ověřte geometrii tranzitního stavu výpočtem frekvencí. Jaká je výška bariéry ve vodě a jaká v chloroformu? Rozpouštědlo modelujte jako kontinuální dielektrikum. V úvodu diskutujte oba mechanismy nukleofilní substituce, vliv rozpouštědla a substituentů. Literatura: E. V. Anslyn, D. A. Dougherty: Modern Physical Organic Chemistry. University Science Books, Sausalito, 2006. | 3G |
| q08 | Solvatace a tautomerní rovnováha | Studujte vliv vody na rovnováhu mezi 2-hydroxypyridinem a 2-pyridonem. Pro zahrnutí vlivu solvatace použijte metodu kontinuálního dielektrika. V protokolu stručně diskutujte význam tautomerních rovnováhy v biomolekulárních vědách. | 2G |
| q09 | Rozklad ozónu | Metodami teoretické chemie vypočítejte reakční energii pro reakci chlórového radikálu s ozónem. Dokázali byste vypočítat aktivační energii této reakce a odhad rychlostní konstanty na základě srážkové teorie a teorie tranzitního stavu? V protokolu diskutuje význam této reakce pro chemii atmosféry. | 4G |
| q10 | Bayerovo pnutí | Vypočítejte hydrogenační entalpie pro cyklopropan, cyklobutan, cyklopropan a cyklohexan. Definujte pojem Bayerovo pnutí a v protokolu se stručně zmiňte o životě a díle A. Bayera. | 2G |
| q11 | Azulen a naftalen | Vypočítejte excitační energie a dipólové momenty azulenu a naftalenu pomocí se- miempirické metody ZINDO. Jakou barvu by měly mít tyto dvě sloučeniny? Jaká je izomerizační energie pro tyto sloučeniny? V úvodu diskutujte Jablonského diagram, včetně Kashových–Vavilovových pravidel (které azulen narušuje). | 3G |
| q12 | Konjugované polyeny | Metodou ZINDO vypočítejte, jak se mění poloha prvního absorpčního pásu pro konjugované polyeny, počínaje ethenem a konče 1,3,5,7,9-dekapentaenem. V úvodu pojednejte o významu fotochemie dvojné vazby, o fotochemii spojené se zrakovým vjemem a o úloze mrkve ve výživě obyvatelstva. | 3G |
| q13 | Dielsova–Alderova reakce | 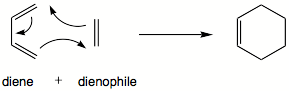 Butadien může reagovat s ethylenem za uzavření cyklu (Dielsova-Alderova reakce). Reakce probíhá synchronním mechanismem a tudíž musí být butadien orientován v poloze „cis“. Najděte substituent R, pro který bude cis forma butadienu stabilnější. Hledejte mezi alkylovými, alkoxy a halogen substituenty. V úvodu pojednejte o syntetických aplikacích Dielsovy-Alderovy reakce. (Obrázek: Wikipedia) Butadien může reagovat s ethylenem za uzavření cyklu (Dielsova-Alderova reakce). Reakce probíhá synchronním mechanismem a tudíž musí být butadien orientován v poloze „cis“. Najděte substituent R, pro který bude cis forma butadienu stabilnější. Hledejte mezi alkylovými, alkoxy a halogen substituenty. V úvodu pojednejte o syntetických aplikacích Dielsovy-Alderovy reakce. (Obrázek: Wikipedia) | 3G |
| q14 | Konstanty kyselosti methylaminů | Vypočítejte pKa v plynné fázi a ve vodě pro primární a sekundární methylaminy. Rozpouštědlo modelujte coby kontinuální dielektrikum. V úvodu diskutujte pojmy „kyseliny slabé a silné“, superkyseliny a fotokyseliny. | 4G |
| q15 | Adenin a thymin | Vypočítejte geometrii adeninu a thyminu v kanonické formě a geometrii vodíkově vázaného komplexu mezi těmito bázemi. Vypočítejte energii vodíkové vazby páru A–T. V úvodu diskutujte význam vodíkové vazby v biologii. | 4G |
| q16 | Optická aktivita | Pomocí semiempirické metody PM3 vypočítejte strukturu pentahelicenu. Pro tuto strukturu vypočítejte optickou otáčivost (pozn. výpočet je náročnější, proto váš vstupní soubor zašlete Petrovi Slavíčkovi, který jej spustí na počítačovém klastru Ústavu fyzikální chemie). Hodnotu optické otáčivosti porovnejte s hodnotou pro kyselinu mléčnou. V úvodu pojednejte o významu chirality v chemii a o chemii helicénů. | 3G |
| q17 | Disociace NaCl | Na jaké fragmenty bude disociovat NaCl v plynné fázi a na jaké ve vodě? Rozpouštědlo modelujte jako kontinuální dielektrikum. Kolik molekul je třeba, aby došlo k disociaci molekuly NaCl? Jakou barvu by měla molekula NaCl v plynné fázi? Literatura: J. Phys. Chem. A 104 (2000) 145. | 3G |
| q18 | Formy síry a fosforu | Vypočítejte energetiku procesů, kdy z atomů síry a fosforu vznikají jejich molekuly. Uvažujte velikost 1–8. Jaká je struktura těchto agregátů? V úvodu diskutuje různé formy síry a fosforu v pevné i v plynné fázi. | 4G |
| q19 | Vlastnosti kyseliny octové | Odhadněte energii spojenou s dimerizací kyseliny octové. Vypočítejte rovnovážnou konstantu dimerizace. Vaše výsledky konfrontujte s experimentem, víte-li, že závislost dimerizační rovnovážné konstanty na teplotě lze vyjádřit vztahem
ln K = 7425,84/T − 29,2438
Jaká část molekul kyseliny octové se bude nacházet ve formě dimeru při pokojové teplotě a atmosférickém tlaku? Vypočítejte dále vibrační frekvenci OH vazby v izolované kyselině octové a v jejím dimeru. Dokázali byste sestrojit stavovou rovnici pro asociující plyn jako kyselina octová? Ze struktury dimeru odhadněte, zdali se budou ve významné míře vytvářet také trimery. | 3G |
| q20 | Struktura aminokyselin | Vypočítejte energii glycinu jako neutrální částice a ve formě zwitteriontu v plynné fázi a v roztoku. Rozpouštědlo popište jako kontinuální dielektrikum. V případě dielektrika vypočítejte obě pKa. V úvodu diskutujte acidobazické vlastnosti aminokyselin. | 5G |
| q21 | Molekuly ve Vesmíru | V mezihvězdném prostoru se může při extrémně nízkých teplotách nacházet ve zmrzlých ledech řada molekul jako oxid uhličitý, voda, karbonylsulfid, bifenyl nebo amoniak. Obdrželi jste naměřené IR spektrum takového ledu. Interpretujte jej a vaše tvrzení podložte vypočtenými daty. Zdroj dat: Jan Polena. | 3G |
| q22 | Deštníkový efekt | Molekula amoniaku se může překlopit skrze svou planární formu. Mluvíme o deštníkovém efektu nebo o planární inverzi. Modelujte energetiku tohoto procesu pro amoniak na DFT i korelovaných ab initio úrovních. Nalezněte tranzitní stav a reakční koordinátu. Diskutujte o experimentální detekci tohoto jevu. Dochází k této inverzi při pokojové teplotě? V případě dostatku času zkuste jev modelovat i pro amoniak substituovaný např. methylovou skupinou. Stručně pojednejte o kulturní historii deštníku. | 3G |
| q23 | Syntéza amoniaku v plynné fázi | Katalytické syntéze amoniaku dle Habera a Bosche vděčíme za přežití většiny z 8 miliard současných obyvatel planety. Syntéza amoniaku v plynné fázi takový význam nemá, ale zase se nám lépe zkoumá technikami počítačové chemie. Hwang a Mebel (J. Phys. Chem. A 2003, 107, 2865–2874) navrhli následující mechanismus:
N2 + H2 → NNH2
NNH2 + H2 → H2NNH2
H2NNH2 → HNNH3
HNNH3+ H2 → NH3 + NH3
Vypočítejte na B3LYP/6-31+g* úrovni energetiku jednotlivých reakčních kroků. První reakce je rychlost určujícím krokem, nalezněte pro ni tranzitní stav a spočítejte aktivační energii. Hodnotu této energie přepočítejte na CCSD(T) úrovni s aug-cc-pVTZ bází. Vypočítejte rovnovážnou konstantu celkové reakce vzniku amoniaku pro 700 K a 1000 K a srovnejte s experimentem. Pro meziprodukty vypočítejte IR spektrum na B3LYP/6-31+g* úrovni. V úvodu se dotkněte etických otázek vědeckého výzkumu na příkladu Fritze Habera. | 4G |
| q24 | Požární chemie |  Látka označovaná jako HFC-227ea (1,1,1,2,3,3,3-heptafluorpropan) se používá jako hasicí činidlo. Je známé také pod označením FM-200. Tato látka má vysokou tepelnou kapacitu a je schopna reagovat s některými volnými radikály. Při vysoké teplotě může ale docházet k eliminaci fluorovodíku za vzniku perfluorpropenu (viz obrázek). Experimentálně byla aktivační energie této reakce stanovena na 291 kJ/mol (měřeno při 1200 K) a reakční entalpie byla stanovena na 146 kJ/mol (při teplotě 298 K). Vypočítejte entalpii reakce pomocí metody B3LYP/6-31g* a srovnejte s energií odhadnutou pomocí průměrných disociačních entalpií vazeb. Vypočítejte tepelnou kapacitu této molekuly a srovnejte s experimentem. Vypočítejte rovnovážnou konstantu reakce při 1200 K. V úvodu pojednejte o vlastnostech tohoto hasicího činidla. Bonus: vypočítejte též aktivační energii této reakce. Látka označovaná jako HFC-227ea (1,1,1,2,3,3,3-heptafluorpropan) se používá jako hasicí činidlo. Je známé také pod označením FM-200. Tato látka má vysokou tepelnou kapacitu a je schopna reagovat s některými volnými radikály. Při vysoké teplotě může ale docházet k eliminaci fluorovodíku za vzniku perfluorpropenu (viz obrázek). Experimentálně byla aktivační energie této reakce stanovena na 291 kJ/mol (měřeno při 1200 K) a reakční entalpie byla stanovena na 146 kJ/mol (při teplotě 298 K). Vypočítejte entalpii reakce pomocí metody B3LYP/6-31g* a srovnejte s energií odhadnutou pomocí průměrných disociačních entalpií vazeb. Vypočítejte tepelnou kapacitu této molekuly a srovnejte s experimentem. Vypočítejte rovnovážnou konstantu reakce při 1200 K. V úvodu pojednejte o vlastnostech tohoto hasicího činidla. Bonus: vypočítejte též aktivační energii této reakce.
| 4G |
| q25 | Montrealský protokol | Látka HFC-227ea zkoumaná v předchozí úloze byla zavedena jako zhášecí plyn nahrazující Halon 1301, který byl opuštěn v důsledku Montrealského protokolu a návazných ujednání v Kodani a Londýně. Zkuste se zamyslet, proč HFC-227ea neničí ozón, zatímco Halon 1301 ano. Vypočítejte disociační energie vazeb v obou molekulách pomocí metody B3LYP/6-31+g* a excitační energii těchto molekul metodou TDDFT se stejným funkcionálem a bází. Charakterizujte elektronové přechody v molekulách. V úvodu mimo jiné pojednejte o boji s úbytkem ozónu. | 4G |
| q26 | Fotopřepínače | Azobenzen patří k nejpoužívanějším fotopřepínačům. Vypočítejte energii E- a Z- azobenzenu. Proveďte optimalizovaný sken mezi těmito formami. Vypočítejte energie základního i dvou excitovaných stavů azobenzenu podél této reakční koordináty metodou ZINDO. Porovnejte izomerizační energie v metodě PM6 a B3LYP/6-31g* s experimentem. Zobrazte molekulové orbitaly a diskutujte o charakteru elektronových přechodů. V úvodu zmiňte použití fotopřepínačů v současných technologiích. | 4G |
| q27 | Sodík ve vodě | Reakce sodíku s vodou stála u zrodu mnoha chemických kariér. Podívejme se na interakci sodíku s klastry vody konečné velikosti. Optimalizujte strukturu Na(H2O)n pro n = 0–4. Vizualizujte vlnovou funkci nejvýše obsazeného (SOMO) orbitalu. Vypočítejte vertikální ionizační energie těchto klastrů. Je možné tuto reakci sledovat pomocí vibrační spektroskopie? V realitě s vodou nereaguje jen jeden atom sodíku. Jaká je vazebná energie molekuly Na2? Srovnejte s molekulou H2. V úvodu vyzvedněte roli elektrochemie pro syntézu prvků a osobnost Humphry Davyho. | 4G |
| q28 | Ztužení helia a vodíku | Zkapalnění helia byl triumf kryogenní vědy přelomu 19. a 20. století, zkapalnit vodík je podstatně snazší. Studujte vazebné křivky mezi dvěma atomy vodíku a dvěma molekulami vodíku (v kolineárním i kolmém uspořádání). Studujte také ionizační energii a polarizovatelnost vodíku a helia. K výpočtům vazebné energie použijte metodu CCSD(T)/aug-cc-pVQZ. V úvodu stručně pojednejte o teorii disperzních sil a historii zkapalňování. | 2G |
| q29 | Vlastnosti histidinu | Vypočítejte rovnovážné konstanty disociace histidinu do jednotlivých stupňů ve vodě (pK1, pK2, pK3). Na základě zjištěných hodnot odhadněte isoelektrický bod histidinu. V úvodu pojednejte o významu acidobazických vlastností histidinu v biochemii dýchání (tzv. Bohrův efekt). Diskutujte o vlivu reprodukčních schopností Christiana Bohra na vývoj kvantové mechaniky. Bonus: Vypočítejte UV-Vis absorpční spektra zwitteriontových forem histidinu, fenylalaninu, tryptofanu a tyrosinu. Jaké jsou příspěvky jednotlivých aminokyselin k absorpci polypeptidů při 280 nm? | 5G |
| q30 | Deaminace nukleových bází | Deaminace cytosinu probíhá za fyziologických podmínek mnohem rychleji než deaminace adeninu. Uracil vzniklý touto deaminací je účinně rozpoznáván opravnými enzymy, i přesto však touto reakcí může vzniknout bodová mutace. Předpokládá se, že právě proto se v DNA přirozeně vyskytuje thymin namísto uracilu (aby byly „správné“ uracily rozpoznány od produktů deaminace cytosinu, viz např. Acc. Chem. Res. 42, 97–106 (2009). Vypočítejte rovnovážné konstanty deaminace adeninu a uracilu v plynné fázi a ve vodě (při teplotách 300 K). V literatuře vyhledejte údaje o rychlostech těchto reakcí. V úvodu pojednejte o techto i dalších reakcích vedoucích k poškození DNA. | 4G |
| q31 | Výpočetní chemie zachraňuje životy | Azid CH3N3 je explozivní látkou. Naproti tomu CF3N3 je zcela stabilní. Vypočítejte reakční energie a Gibbsovu energie pro reakce, kdy se z těchto dvou azidů odštěpuje molekula dusíku N2. Vypočítejte aktivační energie pro tyto rozpady. Vypočítejte IR spektra těchto molekul. V úvodu rozeberte rozdíl mezi primárními a sekundárními výbušninami a otázky bezpečnosti práce. | 4G |
| s01 | 2D kontaktní úhel | Stanovte pro 2D kapalinu implementovanou v SIMOLANTu kontaktní úhel na přitažlivé stěně v závislosti na (rovnoměrné) hustotě materiálu stěny (rho). Stanovte hustotu, kdy dojde k rozestírání, a porovnejte s rovnovážnou hustotou kapaliny. (Návod) | 2S |
| s02 | 2D kapalina ve štěrbině | Stanovte pro 2D kapalinu implementovanou v SIMOLANTu povrchové napětí a mezifázové napětí kapalina–zeď (vyzkoušejte přitažlivou i odpudivou zeď) alespoň za dvou teplot. Zobrazte a okomentujte hustotní profily. (Návod) | 2S |
| s03 | Kelvinova rovnice ve 2D | Stanovte pro 2D kapalinu implementovanou v SIMOLANTu povrchové napětí a tlak nasycených par jak nad rovinným rozhraním, tak nad kapkou i v kavitě („bublině“). Ověřte platnost 2D verze Kelvinovy rovnice. Zobrazte a okomenujte radiální hustotní profil kapky/kavity. (Návod). | 3S |
| s04 | P–V diagram 2D tekutiny a kritický bod | Nasimulujte několik podkritických izoterem a rovnováhu kapalina–pára a pokuste se určit polohu kritického bodu pro 2D systém implementovaný v SIMOLANTu. (Návod) | 3S |
| s05 | Drcení 2D krystalu. | Pro 2D systém implementovaný v SIMOLANTu stanovte aktivační energii posunu krystalových vrstev. (Návod) | 3S |
| s06 | Druhý viriálový koeficient. | Pro 2D systém implementovaný v SIMOLANTu stanovte druhý viriálový koeficent pro několik teplot „pseudoexperimentálně“ z tlaku (resp. ze Z) a srovnejte s přímým výpočtem. (Návod) | 2S |
| s07 | Aktivační energie difuze. | Pro 2D systém implementovaný v SIMOLANTu stanovte MSD a difuzivitu pro několik teplot a z Arrheniova diagramu vypočtěte aktivační energii. (Návod) | 2S |
| s08 | Soft penetrable disks. | Penetrable spheres je jednoduchý model entropické repulze v koloidní chemii. Vysvětlete, co je to entropická repulze a jak se chová řetězec polymeru v dobrém rozpouštědle. Popište vlastnosti (fáze, strukturu) 2D analogie „propustných disků“ implementované v SIMOLANTu. (Několik tipů) | 3S |
| s09 | Střední kvadratické posunutí. | Střední kvadratické posunutí (Mean Square Displacement) částice je definováno vztahem MSD(t)=⟨[r(0)−r(t)]²⟩. Pro 2D systém stanovte vlastnosti MSD v různých skupenstvích a geometrii. (Několik tipů) | 1S |
| s10 | Kvazikrystaly. |  Seznamte nás s pojmem kvazikrystal a Penroseovo dláždění (Penrose tiling). Pokuste se získat tuto strukturu v simulaci potenciálu se dvěma minimy implemenovanou v SIMOLANTu (autor této úlohy neví, zda to jde). (Několik tipů) Seznamte nás s pojmem kvazikrystal a Penroseovo dláždění (Penrose tiling). Pokuste se získat tuto strukturu v simulaci potenciálu se dvěma minimy implemenovanou v SIMOLANTu (autor této úlohy neví, zda to jde). (Několik tipů) | ?S |
| s11 | Koalescence kapek. | Studujte změnu teploty po koalescenci dvou kapek a srovnejte s teoretickým výpočtem z povrchového napětí a tepelné kapacity. (Návod) | 4S |
| s12 | Vicsekův model. |  Vicsekův model je modelem hejna ptáků nebo ryb. Stanovte fázový diagram Vicsekova modelu v souřadnicích hustota (ρ) a parametr Lagevinova termostatu (τ) (případně lze hýbat i teplotou T a dosahem potenciálu c). Vicsekův model je modelem hejna ptáků nebo ryb. Stanovte fázový diagram Vicsekova modelu v souřadnicích hustota (ρ) a parametr Lagevinova termostatu (τ) (případně lze hýbat i teplotou T a dosahem potenciálu c). | 3S |
| s20 | Bod varu NaCl | Stanovte bod varu NaCl za zvýšeného tlaku přímou metodou – kapalina a pára v rovnováze. Systém musí být větší (aspoň Na256Cl256). Zjistěte alespoň kvalitativně, zda v parách NaCl jsou volné ionty, molekuly NaCl nebo větší klastry a pokuste se strukturu par vysvětlit. (Návod) | 5M |
| s21 | Clapeyronova rovnice | Vypočtěte entalpii tání modelu NaCl a bod tání pro (alespoň) dva různé tlaky a porovnejte s predikcí pomocí Clapeyronovy rovnice. (Návod / data) | 4M |
| s22 | Rovnovážný tvar krystalu | Stanovte metodou simulated annealing (velmi pomalé chlazení) rovnovážný tvar krystalku Na32Cl32 za volných (vakuových) okrajových podmínek. Vznikne pravidelný krystal 4×4×4? Přidejte pojednání o závislosti rovnovážného tvaru krystalu na mezifázovém napětí (Wulffova konstrukce). (Návod) | 2M |
| s23 | Rayleighova nestabilita | Padající čúrek vody se rozpadá na kapky. Nejprve si najděte v literatuře teorii tohoto jevu. Simulujte tento jev pomocí dlouhého válce kapalného argonu (případně vody – další informace na požádání). Vzniknou kapky o teoreticky předpovězené velikosti? Češi: je správně čůrek nebo čúrek? Cizinci: jak se řekne čúrek ve vašem rodném jazyce? (Návod) | 2M |
| s24 | Konstrukce silového pole | Nastavte parametry modelu iontů Na+ a Cl− tak, aby popisovaly dobře jak krystal NaCl tak taveninu. Velikost iontů (σ nebo RvdW) nastavíte podle nalezené experimentální hustoty, hloubku potenciálové jámy (nebo Emin) podle výparné entalpie, poměr velikostí obou iontů ovlivňuje stabilitu krystalu (bod tání). (Konzultace doporučená.) | 5M |
| s25 | Bod tání ledů | Stanovte bod tání hexagonálního (Ih) nebo kubického (Ic) ledu přímou metodou. Použijte model vody TIP4P/2005 (případně OPC nebo Nada–Eerden – více informací na požádání). K dispozici budete mít i krystal ledu s náhodnou orientací protonů. Přidejte stručné pojednání o polymorfismu ledu.(Návod.) | 4M |
| s26 | Sbalování proteinů | Nalezněte v literatuře, která aminokyselina nejsnáze tvoří α-helix, vytvořte oligomer ve vhodném silovém poli a zkuste, zda dostanete α-helix spontánním složením ve vakuu či ve vodném prostředí. Blízkost struktury k α-helixu posuďte podle Ramachandranova diagramu. (Návod) | 4M 4Gr |
| s27 | Rozbalování proteinů | Stáhněte z PDB databáze vhodný menší protein bez disulfidických vazeb, nastavte nábojové stavy aminokyselin podle zvoleného pH nebo doplňte protionty, simulujte ve vodném prostředí a stanovte, zda struktura denaturuje za teploty těla a za teploty 100 °C. Vhodné pro jedince se zkušenostmi se simulacemi biomolekul a znalostí Gromacsu. | 4Gr |
| s28 | Kulová hvězdokupa | Kulová hvězdokupa s dostatečným množstvím hvězd je metastabilní útvar pomalu se „vypařující“ do prostoru. Simulujte hvězdokupu složenou z cca 200–400 hvězd o hmotnosti rovné hmotnosti Slunce v oblasti o velikosti řádově jednotky parseků. Verzi MD programu s opačným znaménkem interakce „nábojů“ dostanete na požádání, můžete si ho také sami napsat. Dokážete získat útvar dostatečně stabilní alespoň stovek milionů let? Přidejte výklad o aplikaci věty o viriálu na rovnováhu klastru. Literatura: V. Vanýsek: Základy astronomie a astrofyziky, Academia, Praha (1980). (Návod) | 5M |
| s29 | Chladniho obrazce | Studujte vibrace plátků grafenu. Vizualizujte tak, aby byly vidět uzlové křivky. Přišroubujte na podstavec rezonanční desku tvaru šestiúhelníku a za pomoci smyčce a prášku nám předveďte Chladniho obrazce; pokud se Vám reálný experiment nepovede, spokojíme se i s nějakým pěkným videem z YouTube. Můžete si také půjčit zařízení vyrobené generacemi studentů v místnosti A402. Vysvětlete souvislosti. Na závěr přidejte několik zajímavostí o grafenu. (Návod) | 2M |
| s30 | Elektroforéza | Simulujte atom Xe ve vodním roztoku LiI, ve kterém teče elektrický proud. Může být atom Xe unášen? (Návod / data, vyžaduje delší běhy) | 4M |
| s31 | Struktura povrchového filmu | Simulujte povrchově aktivní látku (oktanol) na povrchu vody ve slab geometrii. Vhodné silové pole (TraPPE-UA pro alkohol a SPC pro vodu) dostanete na požádání. Měňte pokrytí resp. velikost plochy a všímejte si struktury povrchového filmu (2D plyn, kapalina, krystal). Srovnejte s experimentem. (Konzultace doporučená.) | 4M |
| s32 | Rovnováha kapalina–pára | Stanovte rovnovážný diagram kapalina–pára (modelů) ethanolu (TraPPE-UA) a vody (SPC) za teploty 450 K pomocí simulace vrstvy kapaliny a páry nad kapalinou. (Návod / data, vyžaduje delší běhy) | 4M |
| s33 | Klastry zlata | Vytvořte krystalky zlata ve tvaru dvacetistěnu. Simulujte s potenciálem typu tight-binding. Studujte hustotu ve středu krystalku za nulové teploty v závislosti na počtu atomů. Opakujte podobný pseudoexperiment s argonem; rozdíly vysvětlete. (Volitelné: Zkuste krystalek roztavit a pomalu zchladit – zkrystalizuje opět?) Literatura: J. Chem. Phys. 122, 214722 (2005). (Návod / data) | 3M |
| s34 | Simulovaná ničička | Připravte krystalek ledu v modelu TIP4P/2005 za nízké teploty. Odhadněte rychlost, při které je kinetická energie rovna energii potřebné k roztavení ledíků. Dva ledíky nechte danou rychlostí srazit. Vyzkoušejte nižší i vyšší rychlosti. Při jaké rychlosti začnou odletovat fragmenty resp. jednotlivé molekuly? Jako bonus se můžete zmínit o vaší oblíbené filmové ničičce. (Návod) | 3M |
| s35 | Koalescence kapek | Pokud splynou dvě makroskopické kapky vody, teplota se prakticky nezmění. U velmi malých kapek to však neplatí. Vypočtěte změnu teploty po splynutí dvou kapek vody po 250 molekulách. Simulujte ten samý jev s modelem SPC/E. (Návod) | 3M |
| s36 | Rozdíl tepelných kapacit | Simulujte vodu (např. model SPC/E) za běžných podmínek za konstantního tlaku a objemu a stanovte rozdíl tepelných kapacit Cpm−CVm jednak přímo (ze simulace při aspoň dvou teplotách v příslušném souboru), jednak ze stavové rovnice (vyberte vhodnou verzi a opět stanovte derivace numericky z několika simulací). Porovnejte s reálným experimentem. Která metoda je přesnější? (Konzultace doporučená.) | 5M |
| s37 | Kapka v elektrickém poli | Simulujte kapku SPC/E vody v silném elektrickém poli. Jak se změní tvar kapky? (Viz též DOI:10.1021/ie404268f a úloha 122.) (Návod) | 3M |
| s38 | Je 'Oumuamua mimozemský kosmický koráb? | Simulujte rotaci podlouhlého tuhého tělesa (kousek diamantu) ve vakuu a stanovte závislost plochy pozorované z jednoho směru na čase. Vyzkoušejte různé počáteční podmínky. Dostanete křivky podobné naměřeným křivkám jasu 'Oumuamuy na čase? (Návod) | 3M |
| s39 | Var modelu vody | Simulujte metodou MD ve slab geometrii vodu TIP4P/2005 (model dodám) s párou za teploty 200 °C a stanovte rovnovážné hustoty a tlak. (Návod) | 3M |
| s40 | Solanka a Debyeova–Hückeova teorie | Simulujte metodou MD zředěný roztok NaCl ve vodě. Zobrazte radiální distribuční funkce Na–Na, Na–Cl a Cl–Cl a diskutujte výsledky. Z koordinačních čísel (vč. H a O i bez) vypočtěte průměrný náboj v kouli o poloměru r okolo iontu a srovnejte s predikcí podle Debyeovy–Hückeovy teorie. (Návod) | 4M |
| s41 | Elektrospinning | Simulujte vrstvu SPC/E vody v silném elektrickém poli a pozorujte vznik Taylorova kužele a vlákna (DOI:10.1021/ie404268f, viz též úloha 118). (Návod) | 3M |
| s42 | Madelungova konstanta | Stanovte Madelungovu konstantu několika iontových krystalů (např. NaCl, CsCl, ZnS, CaF2) metodou Ewaldovy sumace. Konzultace (Jiří Kolafa) je doporučená. | 5M |
| s43 | Voda a solanka v mikrovlnce | Simulujte vodu (SPC/E) a solanku (model JC) v elektrickém poli o frekvenci 2.45 GHz a stanovte rychlost zahřívání. Můžete provést i reálný experiment. Konzultace (Jiří Kolafa) je doporučená. | 5M |
| s44 | Tepelná roztažnost krystalu a skla | Vypočtěte koeficient objemové tepelné roztažnosti fcc krystalu modelu argonu. Roztavte a rychle ochlaďte, aby vzniklo sklo, a výpočet opakujte. Konzultace (Jiří Kolafa) je doporučená. | 4M |
| s45 | Poissonova konstanta zlata a pevnost zlata v tahu | Na fcc krystal modelu zlata v periodických okrajových podmínkách aplikujte různý tlak/tah v různých směrech, spočtěte Poissonovu konstantu a srovnejte s experimentem. Postupně zvyšujte tah a stanovte mez pevnosti. Konzultace (Jiří Kolafa) je doporučená. | 5M |
| s46 | Stabilita nabitých klastrů vody s ionty | Připravte klastr cca 100 molekul vody ve vakuu a ochlaďte. Vyměňte pravidelně blízko povrchu několik molekul za ion (např. Na+), nejprve silně chlaďte a pak pomalu ohřívejte. Při jakém náboji se klastr rozletí (Coulombova nestabilita)? Konzultace (Jiří Kolafa) je doporučená. | 5M |
| p01 | Monte Carlo tuhých koulí | Simulujte metodou MC tekutinu tuhých koulí v periodických okrajových podmínkách. | 3P |
| p02 | Isingův model ve 3D | Napište program pro MC simulaci Isingova feromagnetu na kubické mřížce v periodických okrajových podmínkách. Monitorujte energii a celkovou magnetizaci (=součet všech spinů). Proveďte termální cyklus: pomalý ohřev z nízké teploty na vysokou a zpátky. Všimněte si hystereze. Podaří se vám odhadnout teplotu a druh fázového přechodu? | 5P |
| p03 | Entropická pružina | Simulujte MC metodou zvanou „reptation“ řetízek N atomů s pevnými délkami vazeb. Mezi atomy není (kromě pevných vazeb) žádná interakce. Koncové body jsou však natahovány stejně velkými opačně orientovanými silami ve směru osy x. Stanovte závislost „výchylky pružiny“ ⟨x1 − xN⟩ na síle. | 3P |
| p04 | Simulated annealing | Pracujete v e-shopu, kde stříháte řetízky na kousky různé délky podle požadavků zákazníků. Řetízky máte na rolích o délce 10 m. Každý den dostanete seznam požadavků zákazníků. Napište počítačový program metodou simulovaného žíhání, který navrhne stříhání řetízků na kousky tak, aby se spotřebovalo co nejméně rolí (zbytek z role, který je kratší než nejkratší požadavek, je odpad). - Navrhněte vhodnou hodnotící funkci („interakční energii“) U.
- Navrhněte MC metodu; jeden zkušební krok může být přesun kousku z jedné role na druhou.
- Simulujte za snižující se „teploty“.
| 3P |
| p05 | Problém obchodního cestujícího | Nechť je dána mapa obsahující N měst. Některá města jsou spojena silnicí o známé délce. Pro každá dvě města existuje alespoň jedna cesta po silnici, která je spojuje; těchto cest může být více, přičemž (v této verzi problému obchodního cestujícího) není předem známo, která je nejkratší. Najděte co nejkratší uzavřenou cestu procházející alespoň jednou každým městem.- „Konfigurace“ je tedy posloupnost N nebo více měst, „energie“ je délka trasy.
- Abychom se vyhnuli zachovávání podmínky, že dva sousedící členy posloupnosti musí být spojeny silnicí, můžeme říci, že nejsou-li dvě města spojena, je jejich vzdálenost rovna součtu všech vzdáleností na mapě.
- Zkušební kroky MC simulace musí dovolit i změnu počtu měst na trase (některými městy projdeme vícekrát).
- Jako počáteční „konfiguraci“ zvolte N-tici (1, 2, ..., N).
- Simulujte za snižující se „teploty“.
| 4P |
| p06 | Lagrangeovy body | Lagrangeovy librační body v soustavě Slunce–planeta jsou body, v nichž se malé těleso pohybuje synchronně s obíháním planety. Stabilní body L4 a L5 leží ve vrcholech rovnostranného trojúhelníka se základnou Slunce-planeta.
Napište program pro integraci pohybových rovnic tří těles. Počáteční podmínky zvolte tak, aby planeta obíhala okolo Slunce po kruhové dráze. Těleso o nepatrné hmotnosti umístěte do těsné blízkosti L4 nebo L5 tak, aby obíhalo (téměř) synchronně. Kontrolujte, zda jsou integrály pohybu konstantní. Zkuste vyjít z bodů L1, L2, L3 nebo z náhodného bodu. | 4P |
| p07 | Dopravní zácpa | Simulujte chování aut na silnici za hustého provozu. Předpokládejte, že volné auto se pohybuje rovnoměrně zrychleně (např. 2 m/s2), dokud nedosáhne maximální rychlosti (např. 36 m/s). Pokud řidič uvidí před sebou jiné auto, začne zpomalovat. Bezpečná vzdálenost přitom závisí na rychlosti (např. dráha, kterou auto ujede za 1 s). Zpomalení by mělo záviset i na vzdálenosti (při velmi malé vzdálenosti řidič musí dupnout na brzdu). Celý model by měl obsahovat i prvek náhody (mírně různá zpomalení či zrychlení, různá bezpečná vzdálenost různých řidičů ap.).
Celou simulaci proveďte v periodických podmínkách (okruh) s tím, že na začátku auta stojí.
Při vhodném nastavení parametrů dojde ke vzniku kolon. Místo zácpy se pohybuje opačným směrem než auta. | 4P |
| p08 | Evoluce barevného vidění | Samci amerických opic nerozlišují červenou a zelenou barvu, dvě třetiny samic ano. Toto je důsledkem existence tří alel (označme je A,B,C) pro pigmenty s mírně posunutou spektrální citlivostí. Gen sídlí na pohlavním chromozomu X, který mají samci jen jeden, a proto nemohou červenou a zelenou rozlišit. U samic se sejdou alely dvě; pokud jsou různé, vidí opice barvy, pokud stejné, jsou na tom jako samci. V populaci je všech tří alel stejně – musí tedy existovat mechanismus, který toto rovnoměrné zastoupení udržuje, protože v případě zcela náhodné dědičnosti časem jedna či dvě alely vymizí. Vidět barevně je určitá evoluční výhoda, lze snáze rozlišit různě barevné ovoce. Např. ale barvovidící opice typu AB může mít se samcem A barvoslepého potomka AA, mechanismus udržující rovnoměrné zastoupení alel je tedy jemnější. Viz Vesmír 91, 195 (2012) a Scientific American 4, 40 (2009).
Simulujte tento problém na populaci (alespoň) 10000 opic (5000 samců a 5000 samic) s počátečním zastoupením alel v poměru 2 % A, 49 % B a 49 % C (rozdělte do obou X chromozomů samice a jednoho X samce náhodně). V jedné generaci proveďte náhodné spáření samců se samicemi a narození jednoho potomka. Aby počet opic nerostl, vyhubte vždy 5000 nejstarších opic tak, aby jich zbylo 10000. Tady je však nutno zavést mírnou selekci, např. tak, že barvoslepé opice s určitou pravděpodobností (cca 1 %) zahynou hlady a/nebo nemohou mít potomka. | 3P |
| p09 | Difuzně řízená agregace |  Uvažujte následující model vzniku dendrimerů při elektrolýze. Použít můžete buď 2D nebo 3D prostor a jak pohyb po mřížce (čtvercové nebo hexagonální) tak spojitý popis polohy iontů. Na začátku máte určitý počet (N) iontů, např. rozmístěných náhodně v kruhu, kouli, čtverci aj. Uprostřed máte jeden atom (elektrodu). V jednom kroku simulace každý ion provede Brownův pohyb (difuzi) v náhodném směru a s určitou (poměrně malou) pravděpodobností pohyb směrem k elektrodě. V případě dotyku s elektrodou se „vybije“ a usadí a stane se součástí elektrody. Dále stanovte gyrační poloměr Rg takového dendrimeru, opakujte pro větší množství iontů a z grafu log(N) vs log(Rg) stanovte fraktální dimenzi. Uvažujte následující model vzniku dendrimerů při elektrolýze. Použít můžete buď 2D nebo 3D prostor a jak pohyb po mřížce (čtvercové nebo hexagonální) tak spojitý popis polohy iontů. Na začátku máte určitý počet (N) iontů, např. rozmístěných náhodně v kruhu, kouli, čtverci aj. Uprostřed máte jeden atom (elektrodu). V jednom kroku simulace každý ion provede Brownův pohyb (difuzi) v náhodném směru a s určitou (poměrně malou) pravděpodobností pohyb směrem k elektrodě. V případě dotyku s elektrodou se „vybije“ a usadí a stane se součástí elektrody. Dále stanovte gyrační poloměr Rg takového dendrimeru, opakujte pro větší množství iontů a z grafu log(N) vs log(Rg) stanovte fraktální dimenzi. | 3P |
| p10 | Požár pralesa (buněčný automat) | Uvažujte „les“ na čtvercové mřížce v periodických okrajových podmínkách. Každý vrchol mřížky se může nacházet ve třech stavech: {živý strom, hořící strom, spáleniště}. Nová konfigurace se generuje z předchozí podle pravidel:- Má-li živý strom alespoň jednoho hořícího souseda (ze 4 sousedů), pak vzplane.
- Hořící strom shoří (v následující konfiguraci se změní ve spáleniště).
- Na spáleništi vyroste nový strom s pravděpodobností p.
Vyjděte z konfigurace náhodně rozmístěnými stromy a spáleništi v poměru 1:1 a s několika hořícími stromy. Vhodné p je několik %. | 2P |
| p11 | Optimalizace MC | Stanovte optimální zlomek přijatých posunutí pro simulaci atomu dusíku v tíhovém poli za teploty T = 300 K vzhledem k veličině průměrná výška molekuly, ⟨h⟩. K tomu musíte kromě veličiny ⟨h⟩ stanovit i její chybu vhodnou metodou (např. blokováním) a simulovat pro různá posunutí. | 3P |
| p12 | Původ nerovnosti mezi lidmi | Uvažujte 1000 lidí, z nichž má každý na začátku 1000 $. Jeden krok simulace nechť je:- Vyber náhodně pár lidí a zjisti, kdo je chudší a kdo bohatší.
- Hoď mincí.
- Padne-li hlava, chudší zaplatí bohatšímu 20 % svého majetku (jeho majetek bude 80 % původní hodnoty); padne-li orel, dostane chudší od bohatšího 25 % svého majetku (jeho majetek bude 125 % původní hodnoty).
To vypadá spravedlivě, protože chudší z dvojice s pravděpodobností 50 % svůj majetek zvětší (o 25 %), s pravděpodobností 50 % zmenší, ale jen o 20 %. Proveďte mnoho kroků simulace a seřaďte jmění podle velikosti, nakreslete graf (příp. spočtěte Giniho koeficient) a vysvětlete výsledky. Zkuste měnit konstanty 25 % a 20 %. Můžete zkusit „přerozdělení“ – třeba tak, že se po nějakém počtu kroků všichni s majetkem M > 10 $ zaplatí daň (M−10 $)*0.1 do státní pokladny, která tyto peníze rozdělí.
B.M. Boghosian: The Inescapable Casino, Scientific American 321, 62 (Nov. 2019) | 2P |
| p13 | Simulace epidemie | Uvažujte následující model, který zhruba popisuje šíření epidemie např. chřipky nebo covid-19 a který lze řešit metodou kinetického MC. Máme G skupin (měst), každá má N obyvatel. Obyvatel může být v jednom ze tří stavů: Vnímavý (zdravý ale bez imunity), Nemocný, Imunní. Na začátku je v populaci několik Nemocných. Každý den dojde k následujícím změnám: - Dojde k P párovým interakcím v rámci každého města. Setká-li se Nemocný s Vnímavým, Vnímavý onemocní.
- Dojde k X párovým interakcím mezi různými skupinami (městy) podle stejného pravidla.
- Nemocný se s pravděpodobností C (jako Cure) uzdraví a stane imunním. Alternativně můžete uvažovat délku nemoci D dní.
- Imunní s pravděpodobností F (jako Fade) ztratí imunitu (stane se Vnímavým), F < C; můžete též zkusit F = 0 (trvalá imunita).
Dostanete při vhodném nastavení parametrů opakující se epidemie? | 4P |
| p14 | Simulace hromadné obsluhy | Uloženka obsluhuje jednoho zákazníka jednu minutu, otevřeno má od 8 do 18 h, za tu dobu přijde 500 zákazníků. Zákazníci přicházejí zcela náhodně (rovnoměrné rozdělení) v průběhu celé otvírací doby. Není-li v Uložence volno, čekají ve frontě (mohou čekat i po zavírací době, ale další již nepřicházejí). Simulujte tento proces a stanovte průměrnou dobu čekání zákazníka a pravděpodobnost, že zákazník bude čekat déle než 5 minut. | 2P |
| p15 | Dvojité kyvadlo | Naprogramujte dvojité matematické kyvadlo, tj. hmotný bod zavěšený na hmotném bodu, který je zavěšený na závěsu. Použijte Verletovu metodu a algoritmus SHAKE pro zachování délek vazeb (iterujte do vysoké přesnosti, jinak se nebude zachovávat energie). Pro malé výchylky odvoďte vztah pro frekvence obou vlastních kmitů v závislosti na hmotnostech a délkách závěsů. Kdy bude pohyb periodický a kdy chaotický? Zkuste nastavit takové parametry, aby poměr frekvencí byl poměr zlatého řezu. Můžete ho i vyrobit. Jiné pěkné kyvadlo. | 4P |
| b01 | Vizualizace alfa-helixů | Alfa-helix patří k základním motivům sekundární struktury proteinů. V databázi PDB vyhledejte proteiny, které obsahují alfa-helixy o 5, 7, 9, 11, 13 a 15 reziduích. Změřte euklidovskou délku helixů a vyneste ji do grafu oproti počtu reziduí. | 3W |
| b02 | Balení náhodných sekvencí | Balení proteinů je klíčovým biofyzikálním dějem ve všech živých organizmech. Terciární struktury definují funkci proteinu. V přírodě existuje omezené množství tříd terciárních struktur (několik set), přestože možných proteinových sekvencí je astronomické množství. Vygenerujte 5 náhodných proteinových sekvencí, každou o 150 reziduích. Pomocí modelu AlphaFold (verze 2 nebo 3) predikujte terciární strukturu náhodných proteinů. Diskutujte výsledky. | 3W |
| b03 | Vliv bodové mutace na hydrofobní jádro proteinu | Zvolte si protein s hydrofobním jádrem, jehož experimentálně zjištěný strukturní model je dostupný v PDB s rozlišením alespoň 3,0 Å. Vytvořte tři analogy zvoleného proteinu. Každý analog nechť má jedno reziduum z hydrofobního jádra mutované na serin. Pomocí modelu AlphaFold určete terciární struktury mutovaných analogů. Pomocí vhodné metriky srovnejte struktury mutovaného a nemutovaného proteinu. Diskutujte i přesnost AlphaFold modelu srovnání experiemntální a predikované struktury nemutovaného analogu. | 3W |
| b04 | Vliv bodové mutace na terciární strukturu proteinu | Terciární struktura proteinů je definována složitou sítí nekovalentních interakcí mezi aminokyselinovými zbytky. Pomocí algoritmu AlphaFold predikujte terciární strukturu vámi vybraného proteinu. Vyberte protein o 150–250 reziduích. Predikujte terciární strukturu sady tří až šesti analogů, které v různých polohách obsahují bodovou mutaci na alanin. Určete, které mutace mají nejvýznamější vliv na terciární strukturu. | 3W |
| b05 | Srovnání rengenové krystalografie a strojového učení | Modely strojového učení pro určení terciární struktury proteinů prošly v posledních letech průdkým rozvojem. Vyhledejte pět různých proteinů v PDB, jejichž experimentální strukturní modely mají rozlišení lepší než 2,5 Å. Predikujte jejich terciární strukturu pomocí algoritmu AlphaFold. Pomocí vhodné metriky (např. RMSD) srovnejte struktury poskytnuté krystalograií a strojovým učením. | 2W |
| b06 | Docking ibuprofenu | Ibuprofen patří mezi nejpoužívanější léky proti bolesti. Pomocí nástroje SwissDock analyzujte, jak se váže ibuprofen do proteinu COX-2. Jako výchozí použijte experimentálně zjištěnou strukturu protein-ligandového komplexu (PDB 4PH9) Pomocí vhodné metriky porovnejte predikovanou polohu ligandu s experimentálně určenou polohou. Popište roli dílčích nekovalentních interakcí mezi ligandem a COX-2. Publikace popisující daný komplex. | 4W |
| b07 | Docking imatinibu | Imatinib patří mezi orálně užívané léky účinné proti některým typům nádorů. Pomocí nástroje SwissDock analyzujte, jak se váže imatinib na tyrosin-kinázu c-ABL. Jako výchozí použijte experimentálně zjištěnou strukturu protein-ligandového komplexu (PDB 1IEP) Pomocí vhodné metriky porovnejte predikovanou polohu ligandu s experimentálně určenou polohou. Popište roli dílčích nekovalentních interakcí mezi ligandem a c-ABL. Publikace popisující daný komplex. | 4W |
| b08 | Docking kofeinu | Kofein je alkaloid celosvětově užívaný ke stimulaci centrální nervové soustavy. Pomocí nástroje SwissDock analyzujte, jak se váže kofein do receptoru A2A. Jako výchozí použijte experimentálně zjištěnou strukturu protein-ligandového komplexu (PDB 3RFM). Pomocí vhodné metriky porovnejte predikovanou polohu ligandu s experimentálně určenou polohou. Popište roli dílčích nekovalentních interakcí mezi ligandem a A2A. Publikace popisující daný komplex. | 4W |
| b09 | Docking libovolné molekuly | Docking je výpočetní metoda predikující vazby nízkomolekulární látky do biomolekuly. Pomocí nástroje SwissDock analyzujte, jak se váže ligand do vámi vybraného receptoru. Jako výchozí použijte experimentálně zjištěnou strukturu protein-ligandového komplexu. Pomocí vhodné metriky porovnejte predikovanou polohu ligandu s experimentálně určenou polohou. Popište roli dílčích nekovalentních interakcí mezi ligandem a receptorem | 5W |
| b10 | Vliv bodové mutace na terciární strukturu (MD simulace) | Molekulově dynamické simulace poskytují konformační soubor biomolekul. Zvolte si malý protein o 100 nebo méně reziduích a vyhledejte jeho exprimentálně zjištěnou terciární strukturu takovou, aby měla rozlišení 2,5 Å nebo lepší. Proveďte molekulově dynamickou simulaci proteinu. Proveďte molekulově dynamickou simulaci jeho analogu s vhodně zvolenou bodovou mutací. Mutaci volte tak, aby byl její předpokládaný efekt na terciární strukturu co největší. Vhodnými metrikami popište vliv bodové mutace na strukturu a dynamiku proteinu. | 5W |
| b11 | Sekvenční porovnání peptidových deformyláz | Peptidová deformyláza je první enzym, se kterým přijde většina bakteriálních proteinů do kontaktu. Odstraňuje formylovou skupiny s N-terminálního N-formylmethioninu. Porovnejte primární strukturu peptidových deformyláz ze tří různých organizmů. Např. podle BLAST určete sekundární strukturu proteinů. Viz též DSSP nebo Stride Web interface. | 3W |
| b12 | Sekvenční porovnání tRNA syntetáz | tRNA syntetázy jsou enzymy, které propojují aminokyseliny s příslušnými transferovými RNA, a nepřímo se tak účastní translace. V každé buňce existuje obyčejně 20 tRNA syntetáz, které se dělí do dvou hlavních tříd. Porovnejte primární strukturu peptidových deformyláz ze tří různých organizmů např. pomocí BLAST. Určete sekundární strukturu proteinů např pomocí DSSP nebo Stride Web interface. | 3W |
| b13 | Sekvenční porovnání vybraného proteinu | Primární struktura je hlavní charakteristikou každého biopolymeru. Přestože se primární struktura homologních proteinů může lišit, jejich 3D tvar může být přitom podobný. Porovnejte primární strukturu vámi vybraného proteinu v několika organizmech např. pomocí BLAST. Jako vhodné se nabízí proteiny zapojené do základního metabolismu buněk. Určete sekundární strukturu proteinů např. pomocí DSSP nebo Stride Web interface. | 4W |
| b14 | Analýza sekundární struktury tRNA | Transferové RNA jsou evolučně staré biomolekuly účastnící se translace. Zvolte si transferovou RNA, jejíž terciární struktura je určená experimentálně s rozlišením lepším než 3,5 Å. Predikujte sekundární strukturu tRNA pomocí několika predikčních nástrojů. Výsledky predikčních metod provnejte mezi sebou a srovnejte je s výsledky odvozenými ze známe 3D struktury. Použijte např. R2DT, RNAWebSuite, ViennaRNA nebo RNAstructureWeb. | 2W |
| b15 | Analýza sekundární struktury mRNA | Messengerová RNA slouží jako dočasné uložiště genetické informace. Na rozdíl od relativně jednoduché DNA dvoušroubovice tvoří RNA velké množství strukturních motivů. Vyhledejte sekvenci mRNA, která je ribozomem zpracovávána pomalu. Jako odrazový můstek mohou sloužit sekvence kódující segmenty bohaté na Arg a Lys. Predikujte sekundární strukturu mRNA o délce 20–70 nukleotidů různými predikčními servery (RNAcentral, RNAWebSuite, ViennaRNA nebo RNAstructureWeb a výsledky porovnejte. | 4W |
| b16 | Analýza sekundární struktury ribozymu | Ribozym je molekula RNA s katalytickou funkcí. Zvolte si ribozym, jehož terciární struktura je určena experimentálně s rozlišením lepším než 3,5 Å. Predikujte sekundární strukturu ribozymu pomocí několika predikčních nástrojů. Výsledky predikčních metod provnejte mezi sebou a srovnejte je s výsledky odvozenými ze známe 3D struktury, viz RNAcentral, RNAWebSuite, ViennaRNA nebo RNAstructureWeb. | 2W |
| b17 | Vizualizace ribozomu | Ribozom je velký biomolekulový komplex zodpovědný za syntézu proteinů. Přestože mechanismus translace je v obecných rysech stejný pro všechny organismy, ribozomy se napříč organismy snačně liší. V PDB vyhledejte kompletní strukturní model bakteriálního, kvasinkového a lidského ribozomu. Vytvořte jejich vizualizace v několika reprezentacích. Např. rozlište proteinové a neproteinové části, nebo každou molekulu v chemickém slova smyslu vykreslete jinou barvou. Diskutujte rozdíly mezi ribozomy. | 3W |
| b18 | Stabevní kameny bakteriálního ribozomu | Ribozom je biomolekulový komplex zodpovědný za syntézu proteinů. V bakteriích se skládá z asi 50 ribozomálních proteinů a 3 vláken ribozomální RNA. V PDB vyhledejte strukturní model bakteriálního ribozomu s rozlišením alespoň 3,0 Å. Vytvořte vizualizace celého ribozomu a jeho jednotlivých částí zvlášť. Části ribozomu (ribozomální RNA a proteiny) seřaďte podle různých kritérií, např. počtu reziduí, gyračního poloměru, počtu bazických reziduí, atp. | 3W |
| b19 | Vizualizace proteazomu | Proteazom je biomolekulový komplex zodpovědný za degradaci proteinů. V PDB vyhledejte strukturní model 20S proteazomu s rozlišením alespoň 3,0 Å. Vytvořte vizualizace horizontálního a vertikálního řezu proteazomem. Části proteazomu (proteiny) seřeďte podle různých kritérií, např. počtu reziduí, gyračního poloměru, počtu bazických reziduí, atp. Vytvořte vizualizace horizontálním a vertikálním řezem proteazomu a diskutujte tvar jeho katalytické kavity. | 3W |
| b20 | Vizualizace zvoleného biomolekulového komplexu | Biomolekuly běžně asociují za tvorby funkčních komplexů. V PDB vyhledejte strukturní model vámi vybraného biomolekulového komplexu, který se skládá alespoň z 5 podjednotek (RNA nebo protein) a má rozlišení alespoň 3,5 Å. Vytvořte vizualizace celého biomolekulového komplexu a všech jeho částí zvlášť. Části komplexu seřeďte podle různých kritérií, např. počtu reziduí, gyračního poloměru, počtu bazických reziduí, atp. Vytvořte vizualizace funkčně kritických částí biomolekulového komplexu. | 4W |
| b21 | Vizualizace multidoménového proteinu | Proteiny s dlouhou sekvencí jsou obvykle orgranizované do několika domén. K funkci proteinu pak přispívá jejich vzájemná dynamika. V PDB vyhledejte strukturní model proteinu, který se skládá alespoň ze 3 domén. Typicky půjde o proteiny s délkou sekvence > 500. Vyberte strukturní model, který má rozlišení alespoň 3,5 Å. Vytvořte vizualizace proteinu tak, aby každá doména byla vykreslena jinou barvou. Vytvořte vizualizace funkčně kritických částí biomolekulového komplexu, zvolte vhodnou reprezentaci. | 2W |
| b22 | Vizualizace konformačního souboru | Proteiny jsou dynamické objekty. Některé experimentální metody, např. nukleární magnetická rezonance, poskytují místo statické obrázku konformační soubor biomolekuly. V PDB vyhledejte strukturní model proteinu nebo nukleové kyseliny určený metodou NMR, který obsahuje alespoň 5 konformací. Vytvořte vizualizace biomolekuly tak, aby každá konformace byla vykreslena zvlášť. Konformace seřaďte podle různých kritérií, např. gyračního poloměru, vzdálenosti C- a N- konce, atp. | 2W |
| b23 | Reprezentace terciární struktury proteinu | Terciární struktura má několik úrovní komplexity. V PDB vyhledejte strukturní model proteinu nebo nukleové kyseliny určený metodou rentgenové krystalografie, který má rozlišení 3,0 Å nebo lepší. Vytvořte vizualizace biomolekuly v několika reprezentacích zdůrazňujících různé aspekty terciární struktury. Využijte barevné škály pro vyjádření různých vlastností proteinu. | 1W |
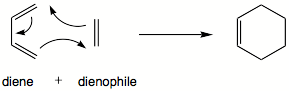 Butadien může reagovat s ethylenem za uzavření cyklu (Dielsova-Alderova reakce). Reakce probíhá synchronním mechanismem a tudíž musí být butadien orientován v poloze „cis“. Najděte substituent R, pro který bude cis forma butadienu stabilnější. Hledejte mezi alkylovými, alkoxy a halogen substituenty. V úvodu pojednejte o syntetických aplikacích Dielsovy-Alderovy reakce. (Obrázek: Wikipedia)
Butadien může reagovat s ethylenem za uzavření cyklu (Dielsova-Alderova reakce). Reakce probíhá synchronním mechanismem a tudíž musí být butadien orientován v poloze „cis“. Najděte substituent R, pro který bude cis forma butadienu stabilnější. Hledejte mezi alkylovými, alkoxy a halogen substituenty. V úvodu pojednejte o syntetických aplikacích Dielsovy-Alderovy reakce. (Obrázek: Wikipedia) Látka označovaná jako HFC-227ea (1,1,1,2,3,3,3-heptafluorpropan) se používá jako hasicí činidlo. Je známé také pod označením FM-200. Tato látka má vysokou tepelnou kapacitu a je schopna reagovat s některými volnými radikály. Při vysoké teplotě může ale docházet k eliminaci fluorovodíku za vzniku perfluorpropenu (viz obrázek). Experimentálně byla aktivační energie této reakce stanovena na 291 kJ/mol (měřeno při 1200 K) a reakční entalpie byla stanovena na 146 kJ/mol (při teplotě 298 K). Vypočítejte entalpii reakce pomocí metody B3LYP/6-31g* a srovnejte s energií odhadnutou pomocí průměrných disociačních entalpií vazeb. Vypočítejte tepelnou kapacitu této molekuly a srovnejte s experimentem. Vypočítejte rovnovážnou konstantu reakce při 1200 K. V úvodu pojednejte o vlastnostech tohoto hasicího činidla. Bonus: vypočítejte též aktivační energii této reakce.
Látka označovaná jako HFC-227ea (1,1,1,2,3,3,3-heptafluorpropan) se používá jako hasicí činidlo. Je známé také pod označením FM-200. Tato látka má vysokou tepelnou kapacitu a je schopna reagovat s některými volnými radikály. Při vysoké teplotě může ale docházet k eliminaci fluorovodíku za vzniku perfluorpropenu (viz obrázek). Experimentálně byla aktivační energie této reakce stanovena na 291 kJ/mol (měřeno při 1200 K) a reakční entalpie byla stanovena na 146 kJ/mol (při teplotě 298 K). Vypočítejte entalpii reakce pomocí metody B3LYP/6-31g* a srovnejte s energií odhadnutou pomocí průměrných disociačních entalpií vazeb. Vypočítejte tepelnou kapacitu této molekuly a srovnejte s experimentem. Vypočítejte rovnovážnou konstantu reakce při 1200 K. V úvodu pojednejte o vlastnostech tohoto hasicího činidla. Bonus: vypočítejte též aktivační energii této reakce. Seznamte nás s pojmem kvazikrystal a Penroseovo dláždění (Penrose tiling). Pokuste se získat tuto strukturu v simulaci potenciálu se dvěma minimy implemenovanou v SIMOLANTu (autor této úlohy neví, zda to jde). (Několik tipů)
Seznamte nás s pojmem kvazikrystal a Penroseovo dláždění (Penrose tiling). Pokuste se získat tuto strukturu v simulaci potenciálu se dvěma minimy implemenovanou v SIMOLANTu (autor této úlohy neví, zda to jde). (Několik tipů) Vicsekův model je modelem hejna ptáků nebo ryb. Stanovte fázový diagram Vicsekova modelu v souřadnicích hustota (ρ) a parametr Lagevinova termostatu (τ) (případně lze hýbat i teplotou T a dosahem potenciálu c).
Vicsekův model je modelem hejna ptáků nebo ryb. Stanovte fázový diagram Vicsekova modelu v souřadnicích hustota (ρ) a parametr Lagevinova termostatu (τ) (případně lze hýbat i teplotou T a dosahem potenciálu c). Uvažujte následující model vzniku dendrimerů při elektrolýze. Použít můžete buď 2D nebo 3D prostor a jak pohyb po mřížce (čtvercové nebo hexagonální) tak spojitý popis polohy iontů. Na začátku máte určitý počet (N) iontů, např. rozmístěných náhodně v kruhu, kouli, čtverci aj. Uprostřed máte jeden atom (elektrodu). V jednom kroku simulace každý ion provede Brownův pohyb (difuzi) v náhodném směru a s určitou (poměrně malou) pravděpodobností pohyb směrem k elektrodě. V případě dotyku s elektrodou se „vybije“ a usadí a stane se součástí elektrody. Dále stanovte gyrační poloměr Rg takového dendrimeru, opakujte pro větší množství iontů a z grafu log(N) vs log(Rg) stanovte fraktální dimenzi.
Uvažujte následující model vzniku dendrimerů při elektrolýze. Použít můžete buď 2D nebo 3D prostor a jak pohyb po mřížce (čtvercové nebo hexagonální) tak spojitý popis polohy iontů. Na začátku máte určitý počet (N) iontů, např. rozmístěných náhodně v kruhu, kouli, čtverci aj. Uprostřed máte jeden atom (elektrodu). V jednom kroku simulace každý ion provede Brownův pohyb (difuzi) v náhodném směru a s určitou (poměrně malou) pravděpodobností pohyb směrem k elektrodě. V případě dotyku s elektrodou se „vybije“ a usadí a stane se součástí elektrody. Dále stanovte gyrační poloměr Rg takového dendrimeru, opakujte pro větší množství iontů a z grafu log(N) vs log(Rg) stanovte fraktální dimenzi.